Question

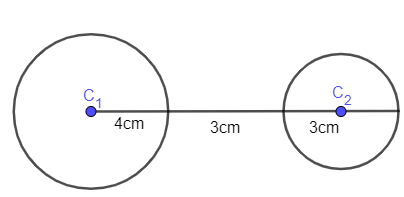
Find the length of the transverse common tangent.
(a) \[5\sqrt{2}\]
(b) 7
(c) \[\sqrt{55}\]
(d) \[\sqrt{51}\]

Answer 1

Hint: Transverse common tangent (TCT) meets on the line passing through the centre. Find the distance between the centre of the circle and mark it as ‘ \[\lambda \] ‘. Thus substitute the value of \[\lambda \] and the radius of both circles to the equation of length of TCT.

Complete step-by-step answer:
A common tangent is a line that is tangent to two circles. Now a transverse common tangent meets on the line passing through the centre and divides it internally in the ratio of radii as shown in figure.

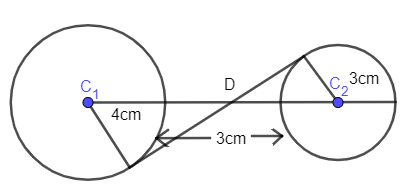
So, let us mark D as the point where the common tangent meets the line passing the centre of the circle.
We have been given the two circles as \[{{C}_{1}}\] and \[{{C}_{2}}\] . The radius of both the circles can be marked as \[{{r}_{1}}\] and \[{{r}_{2}}\] . Let us mark ‘d’ as the distance between the centre of the circles.
The length of a transverse common tangent to two circles is given by the formula,
Length of a transverse common tangent \[=\sqrt{{{d}^{2}}-{{\left( {{r}_{1}}+{{r}_{2}} \right)}^{2}}}\] ……………………(i)
Here, we know ‘d’ as the distance between centres. Hence, from the figure
\[\lambda =4+3+3=10cm\]
d=10cm
Now let us apply all the values in (i)
Length of a transverse common tangent \[=\sqrt{{{\left( 10 \right)}^{2}}-{{\left( 4+3 \right)}^{2}}}\]
\[=\sqrt{100-{{\left( 7 \right)}^{2}}}=\sqrt{100-49}=\sqrt{51}\]
Hence, we got the length of the transverse common tangent as \[\sqrt{51}\] .
\[\therefore \] option (d) is correct.

Note: In the circle \[{{C}_{2}}\] , we might by mistake take 3cm as the diameter of the circle, whereas 3cm is the radius of the circle. The portion of tangent is important, so try to learn the formula.