Question

How do I find the length of the side of the equilateral triangle given only altitude which is \[12\sqrt{3}\]?

Answer 1

Hint: Equilateral triangle contains three equal sides. Let us consider ‘x’ to be the length of the equilateral triangle which has to be found out. Given, the altitude is \[12\sqrt{3}\]. Using Pythagoras formula, we get a quadratic equation with variable x. Solve the quadratic equation and find the value of ‘x’ which is the required final answer.

Complete answer:
According to the question, we are asked to find the length of the equilateral triangle.
We have been given that the altitude of the given equilateral triangle is \[12\sqrt{3}\].
Let ‘x’ be the sides of the equilateral triangle and h be the altitude such that \[h=12\sqrt{3}\].
Let us now draw the equilateral triangle with the given and assumed values.

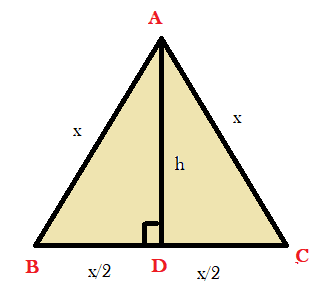
Here, AB=BC=AC=x
And since the altitude divides the base BC into half, we get,
BD=DC=\[\dfrac{x}{2}\].
Also, AD=h=\[12\sqrt{3}\].
Now let us consider the triangle ABD.
Since ABD is a right-angled triangle, we can use Pythagoras formula.
 That is,
\[{{\left( Hypotenuse \right)}^{2}}={{\left( \text{adjacent side} \right)}^{2}}+{{\left( base \right)}^{2}}\]
Here, hypotenuse=AB, base=BD and adjacent side=AD.
Therefore, using Pythagoras formula in triangle ABD, we get,
\[{{\left( AB \right)}^{2}}={{\left( AD \right)}^{2}}+{{\left( BD \right)}^{2}}\] -------(1)
We know the values of AB, AD and BD.
Substituting theses values in formula (1), we get,
\[{{x}^{2}}={{\left( 12\sqrt{3} \right)}^{2}}+{{\left( \dfrac{x}{2} \right)}^{2}}\]
On further simplification, we get,
 \[{{x}^{2}}={{\left( 12 \right)}^{2}}{{\left( \sqrt{3} \right)}^{^{2}}}+\dfrac{{{x}^{2}}}{{{2}^{2}}}\].
We know that \[{{\left( 12 \right)}^{2}}=144,{{\left( \sqrt{3} \right)}^{^{2}}}=3\] and \[{{2}^{2}}=4\].
We get,
\[{{x}^{2}}=\left( 144 \right)\left( 3 \right)+\dfrac{{{x}^{2}}}{4}\]
\[\Rightarrow {{x}^{2}}=432+\dfrac{{{x}^{2}}}{4}\].
Let us divide the whole equation by 4. We get,
\[4{{x}^{2}}=4\left( 432 \right)+\dfrac{{{x}^{2}}}{4}\times 4\]
On further simplifications,
\[\Rightarrow 4{{x}^{2}}=4\left( 432 \right)+{{x}^{2}}\]
\[\Rightarrow 3{{x}^{2}}=4\left( 432 \right)\]
Divide the whole equation by 3. We get,
\[\Rightarrow \dfrac{3{{x}^{2}}}{3}=\dfrac{4\left( 432 \right)}{3}\]
\[\Rightarrow {{x}^{2}}=\dfrac{4\left( 144\times 3 \right)}{3}\]
 \[\Rightarrow {{x}^{2}}=4\times 144\]
Taking square root on both the sides, we get,
\[\sqrt{{{x}^{2}}}=\sqrt{4\times 144}\]
\[\Rightarrow \sqrt{{{x}^{2}}}=\sqrt{4}\times \sqrt{144}\]
\[\Rightarrow \sqrt{{{x}^{2}}}=\sqrt{{{2}^{2}}}\times \sqrt{{{\left( 12 \right)}^{2}}}\]
We know that \[\sqrt{{{a}^{2}}}=a\].
Using this property in the above obtained equation, we get
  \[x=2\times 12\]
\[\therefore x=24\]
Therefore, the length of the equilateral triangle is 24.
Hence, the length of the side of the equilateral triangle given only altitude which is \[12\sqrt{3}\] is 24.

Note: In this type of question, we have to use Pythagoras formula. We should make all the calculations carefully so that we get the answer accurately. We should not make calculation mistakes with sigh conventions. Also knowing the square root of basic numbers, we can easily solve.