Question

Find the length of the diagonal of the rectangle whose length is $8$ cm and width is $6$ cm.

Answer 1

Hint: For finding the length of diagonal of rectangle, we will use the Pythagorean Theorem that is $lengt{{h}^{2}}+widt{{h}^{2}}=diagona{{l}^{2}}$ because each angle of rectangle is a right angle and a diagonal divides the rectangle into two equal triangles.

Complete step by step solution:
We consider that $\square ABCD$ is a rectangle and $BD$ is its diagonal.

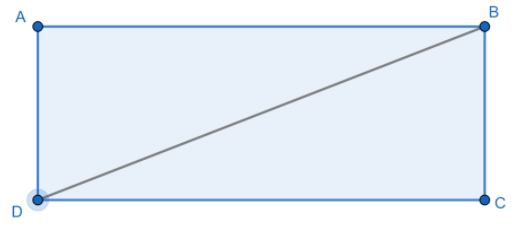
It is given that $AB=8$ cm and $BC=6$ cm.
Let’s take a triangle $\Delta ABD$, where $\angle A$ is a right angle.
Then, from Pythagorean Theorem, we have the formula as:
$\Rightarrow B{{D}^{2}}=A{{B}^{2}}+A{{D}^{2}}$
According to the property of rectangle, we can say that:
$\Rightarrow BC=AD=6$ cm.
Now, we will substitute the corresponding values in the Pythagorean Theorem as:
$\Rightarrow B{{D}^{2}}={{8}^{2}}+{{6}^{2}}$
Here, we will get $64$ and $36$ after squaring $8$ and $6$ respectively. So, the above equation will be as:
  $\Rightarrow B{{D}^{2}}=64+36$
We will have $100$ after adding $64$ and $36$ in the above step as:
$\Rightarrow B{{D}^{2}}=100$
As we know, $100$ is a square of $10$. So, we can write the above step as:
$\Rightarrow B{{D}^{2}}={{10}^{2}}$
Now, we will take square root both sides in the above step and will get the above step as:
$\Rightarrow BD=10$
Hence, the diagonal of the rectangle is $10$ cm.

Note: A rectangle is a type of polygon with four sides and four right angles. So, it is a form of a quadrilateral. In a rectangle length is greater than width always and the area of the rectangle is the product of its length and width.