Question

Find the length of the diagonal of a rectangle whose sides are 21 cm and 20 cm.

Answer 1

Hint: In a rectangle, length, breadth and diagonal always form a right angled triangle. Analyze the given situation with a diagram and use Pythagoras theorem to find the length of the diagonal.

Complete step by step answer:
According to the question, the two sides of the rectangle are 21 cm and 20 cm. Let the length of the rectangle is 21 cm, its breadth is 20 cm and its diagonal is D as shown in the figure. Then we have:
$l = 21cm,b = 20cm$ ,

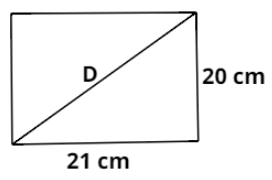
Now, as per the property of the rectangle, the length, breadth and diagonal always form a right angled triangle with diagonal as the hypotenuse. Then applying Pythagoras theorem, we’ll get:
$
   \Rightarrow {D^2} = {l^2} + {b^2} \\
   \Rightarrow {D^2} = {21^2} + {20^2} \\
   \Rightarrow {D^2} = 441 + 400 \\
   \Rightarrow {D^2} = 841 \\
$
Taking square root on both sides, we’ll get:
$
   \Rightarrow D = \sqrt {841} \\
   \Rightarrow D = 29cm \\
$

Thus the length of the diagonal of the rectangle is 29 cm.

Note: A diagonal always divides the rectangle into two congruent right angled triangles. Two intersecting diagonals, on the other hand, divide the rectangle into four congruent triangles. If in place of a rectangle, a square of side s is given, then the length of its diagonal will be $s\sqrt 2 $.