Question

Find the length of the altitude of an equilateral triangle, each side measuring ‘a’ units.
a)${\displaystyle \frac{\sqrt{2}a}{2}}$
b)${\displaystyle \frac{\sqrt{3}a}{2}}$
c)${\displaystyle \frac{\sqrt{7}a}{2}}$
d)${\displaystyle \frac{\sqrt{5}a}{2}}$

Answer 1

Hint: The altitude of an equilateral triangle bisects the base and we can say that this altitude converts the equilateral triangle into two right angled triangles. Now, using pythagoras theorem, we will find the altitude of the equilateral triangle.

Complete step-by-step answer:
It is given in the question that we have to find the altitude of an equilateral triangle having side measuring ‘a’. We will first assume that ABC is an equilateral triangle and AD is an altitude on side BC in triangle ABC.

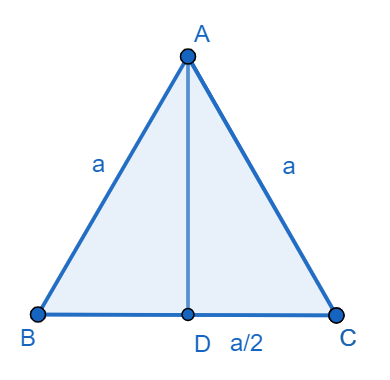
We know that the altitude of the equilateral triangle bisects the base which means altitude from A to BC bisects BC, therefore we get $BD=CD={\displaystyle \frac{a}{2}}$. Now, we have two right angled triangles $\mathrm{\Delta }ADB$ and $\mathrm{\Delta }ADC$. In $\mathrm{\Delta }ADB$, we will apply Pythagora's theorem. Basically pythagoras theorem states that in a right angled triangle the sum of squares of height and base is equal to the square of hypotenuse, that is, ${\left(height\right)}^2+{\left(base\right)}^2={\left(hypotenuse\right)}^2$.
Therefore, in $\mathrm{\Delta }ADB$, we have ${\left(AB\right)}^2={\left(BD\right)}^2+{\left(AD\right)}^2$. We have $AB=a$ and $$BD={\displaystyle \frac{a}{2}}$$ thus, transposing the terms in the pythagoras theorem equation, we get ${\left(AD\right)}^2={\left(AB\right)}^2-{\left(BD\right)}^2$. Putting the values in these equation we get ${\left(AD\right)}^2={\left(a\right)}^2-{\left({\displaystyle \frac{a}{2}}\right)}^2$ simplifying further we get ${\left(AD\right)}^2={\left(a\right)}^2-\left({\displaystyle \frac{a^2}{4}}\right)$ therefore simplifying further ${\left(AD\right)}^2={\displaystyle \frac{4a^2-a^2}{4}}={\displaystyle \frac{3a^2}{4}}$. Finally we get the length of altitude of an equilateral triangle as $AD=\sqrt{{\displaystyle \frac{3a^2}{4}}}={\displaystyle \frac{\sqrt{3}a}{2}}$.
Therefore for an equilateral triangle having each side equal to a, we get a length of an altitude as ${\displaystyle \frac{\sqrt{3}a}{2}}$ thus option b) is the correct answer.

Note: Usually students don't know that the altitude of an equilateral triangle bisects the base thus they get stuck initially. Even many student do mistakes in calculation in plus and minus and in last step may skip to find the root of 4 in hurry they may write $${\left(AD\right)}^2={\displaystyle \frac{\sqrt{3}{a}^2}{4}}$$ which is not correct. Thus it is recommended to solve carefully.