Question

How do you find the length of a rectangle whose diagonal has a length of 10cm and whose width is 5cm.

Answer 1

Hint: We know the length of the diagonal and the width of the rectangle from the question. To be able to solve the question, drawing a figure would be helpful. Once we draw the figure, we can apply Pythagoras theorem to one of the right-angled triangles to find the length.

Complete Step by Step Solution:
From the question,
Length of the diagonal of the rectangle = 10cm
Width of the rectangle = 5cm
Let the length of the rectangle be x cm.
All angles of the rectangle are right angles. Therefore, we can form two congruent right-angled triangles by drawing one of the diagonals.

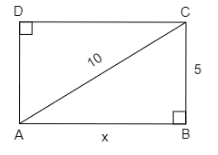
Consider the right-angled triangle ABC.
Using Pythagoras theorem,
$\Rightarrow {(AC)^2} = {(AB)^2} + {(BC)^2}$
Substituting the value of AC as 10cm, the value of BC as 5cm, and the value of AB as x cm, we get
$\Rightarrow {(10)^2} = {(5)^2} + {(x)^2}$
$\Rightarrow 100 = 25 + {x^2}$
Taking 25 to the other side and simplifying,
$\Rightarrow 100 - 25 = {x^2}$
$\Rightarrow {x^2} = 75$
To find the value of x, we need to take the square root of 75,
$\Rightarrow x = \sqrt {75}$
In order to find the square root, 75 needs to be written in terms of its factors, i.e.,
$\Rightarrow 75 = 5 \times 5 \times 3 = {5^2} \times 3$
Therefore, $\sqrt {75} = \pm 5\sqrt 3$ .
However, the negative root cannot be used as the distance is always a positive quantity. Hence, $x = 5\sqrt 3$ .
$\sqrt 3$ can be approximated as 1.732, thus making the value of $x = 5 \times 1.732 = 8.66cm$ (approximately).

This implies that the value of AB is 8.66cm and thus the length of the rectangle is 8.66cm.

Note:
Common errors and misconceptions
While solving the question, one might label the sides incorrectly which causes difficulty in solving the question and eventually leads to the wrong answer. An important concept to be kept in mind is that the hypotenuse will always be the side opposite the right angle.
Another common error is forgetting to square the sides while starting the calculation or forgetting to find the square root value at the end.
One might get confused if the figure used is rotated at different angles, i.e., adding instead of subtracting or adding the wrong sides.