Question

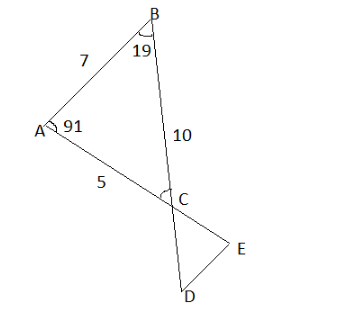
Find the length EC

 $
  A.{\text{ 5}} \\
  {\text{B}}{\text{. 6}} \\
  {\text{C}}{\text{. 7}} \\
  {\text{D}}{\text{. 10}} \\
  $

Answer 1

Hint: Here, we will use the fundamental concept of the similar triangles, and the ratio of the given two sides for the third unknown length of the other triangle. Place the value and find out the scale factor.

Complete step-by-step answer:
By using the definition of the similar triangles – it states that if an angle of one triangle is congruent to the corresponding angle of the other triangle and the lengths of the sides including angles are in proportion , then the given two triangles are similar.
\[\Delta ABC{\text{ and }}\Delta {\text{EDC}}\]are the similar triangles. Where A corresponds to E, B corresponds to D and C corresponds to C.
In similar triangles, the corresponding sides of the triangle are in proportion.
Now, we will find the scale factor from the given measurements.
Line AC and BC meets at a point,
The scale factor is found that C divides BC and AC at a point.
Scale factor $ = \dfrac{{10}}{5} $
Scale factor $ = 2 $
It implies that one triangle is twice the other triangle.
Use the same scale factor to find the length of EC, since E corresponds to A and C corresponds to C.
Therefore, $ \Rightarrow EC = 2 \times 5 = 10 $
Hence, the required answer – the length of EC $ = 10 $
So, the correct answer is “Option D”.


Note: The concept of the similar triangles can be applied and identified easily. The three basic methods state Angle-angle (AA), side-angle-angle (SSA) and side-side-side (SSS) for determining the similarity in triangles. Remember that if two pairs of the corresponding angles in the pair of triangles are congruent, then the triangles are known as the similar triangles.