Question

Find the least number of cuts required which can cut a cube into \[60\] identical pieces?
A. \[9\]
B. $ 12 $
C. $ 15 $
D. $ 5 $

Answer 1

Hint: We know that whenever a three dimension symmetrical figure is cut along any axis, it always gives one plus identical figures. Hence, to find number of cuts required for \[60\] identical pieces, we will equate \[60\] with $ (m + 1)(n + 1)(p + 1) $ , where $ (m + 1),\,(n + 1)\,and\,(p + 1) $ identical pieces are obtained when a cut is made along x-axis, y-axis and z-axis.

Complete step-by-step answer:
Let consider a cube of any side. As we know that cube is a three dimension symmetrical figure.
To get identical figures on cut. We know that there are two ways to cut. One along the x-axis and other along y-axis. But if we cut any figure in a slant way, the result will not be a symmetrical figure every time.
So, for a cube if we cut only one time along the x-axis, then there will be two identical figures obtained after a cut.

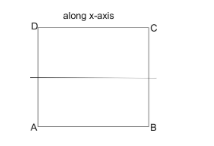
But, if we cut two times then there will be three identical figures as a result.
And for three times we will get four figures.

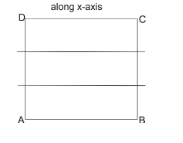
Then, from above we see that on cutting a cube ‘m’ times along the x-axis then we will obtain $( m + 1) $ identical figures as result.
Also, if we make two cuts one along x-axis and other along y-axis at same time. Then we will get double the identical figures that we discussed above.

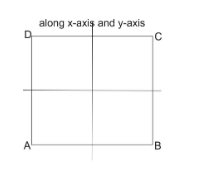
And, if we cut a cube two times along x-axis and two times along y-axis. Then there will be $ 9 $ identical figures obtained as a result. We know that whenever a three dimension symmetrical figure is cut along any axis, it always gives one plus identical figures. Hence, to find number of cuts required for \[60\] identical pieces, we will equate \[60\]with $ (m + 1)(n + 1)(p + 1) $ , where $ (m + 1),\,(n + 1)\,and\,(p + 1) $ identical pieces are obtained when a cut is made along x-axis, y-axis and z-axis.
Hence, from above we see that the total number of identical pieces of a figures when we make a cut along x-axis and y-axis is given as a product of identical pieces obtained from cuts along x-axis and y-axis.
Therefore, a number of identical pieces when cuts are made along x-axis and y –axis are given as = (m+1)(n+1), where ‘m’ are cuts along x-axis and ‘n’ are cuts along y- axis.
Therefore, in the first case if there are cuts along the x-axis and y- axis made on a cube. Then there would be four identical figures. Which is double of the case we got earlier in the first case.
In the same way if we make three cuts one along x-axis, one along y-axis and one along z-axis. Then, total number of identical pieces will be given as = $ (m + 1)(n + 1)(p + 1) $
But, in a given problem it is given that a total number of identical figures are required.
So, we have to calculate the minimum numbers of cuts required.
  $ (m + 1)(n + 1)(p + 1) = 60 $
Now, to get the value of three variables m, n and p. We write $ 60 $ as a product of three consecutive numbers in any order.
We can write $ 60 $ as \[3 \times 4 \times 5\,\,or\,5 \times 4 \times 3\,\,or\,4 \times 3 \times 5\,\] any many others.
But, the result can be obtained by using either, as the cube is a three dimensional symmetrical figure.
Therefore, form above we have:
 $ \left( {m + 1} \right)\left( {n + 1} \right)\left( {p + 1} \right) = 3 \times 4 \times 5 $
Comparing respective terms of above product we have
 $
 m + 1 = 3,\,\,\,\,\,\,\,n + 1 = 4\,\,\,\,and\,\,\,p + 1 = 5 \\
 \Rightarrow m = 2,\,\,\,\,\,\,\,n = 3\,\,and\,\,p = 4 \;
 $
Therefore, number of minimum cuts are given $ 2 + 3 + 4 = 9 $
So, the correct answer is “Option A”.

Note: Identical figures can only be obtained by cutting them along perpendicular lines means along x-axis and y-axis. If we cut along a slant direction maybe we get identical figures at one step or two but not more. So, to obtain identical figures of given figures one should cut it along the x-y plane always.