Question

Find the least number by which \[200\] must be multiplied to make it a perfect square.

Answer 1

Hint: A perfect square is a number which has all its prime factors in pairs. We will divide $200$ by the smallest prime number. We will use the same approach to calculate it further. A prime factor is a factor of the given number which is a prime number also.

Complete step by step answer:
(1) Given number is\[200\]
Making prime factors of\[200\].

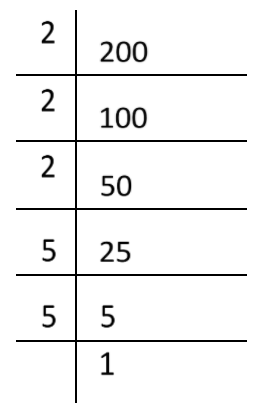
 Or \[200=2\times 2\times 2\times 5\times 5\]
(2) Writing in pair
\[200=2\times 2\times 5\times 5\times 2\]
(3) In the above step, we see that there is only one number $2$ which does not have its pair. We can see that other numbers such as 5 and other 2 have pairs.
Therefore, we can say that \[200\] is not a perfect square number.
(4) Now to make \[200\], a perfect square number, we need to multiply 200 in such a manner that it completes its pair which is not other than $2$.
(5) Therefore by multiplying \[200\] by $2$, we get the following prime factors \[2\times 2\times 5\times 5\times 2\times 2\]
(6) We see all the prime factors \[200\] are now in pairs.
Therefore, multiplying \[200\] by \[2,\,200\] becomes $400$ is a perfect square.
(7) Therefore, the least number we require to make \[200\] a perfect square is $2$. The perfect square is $400$.

Note: A square number or perfect square is an integer that is a square of an integer; in other words, it is the product of some integer with itself. Taking the square root of a perfect square always gives us an integer.