Question

Find the LCM of 12, 36 and 160 by prime factorization method.

Answer 1

Hint: By using prime factorization, split the given number as a product of prime numbers. Thus, from three prime numbers find the LCM taking the common term together and multiply together the rest of the terms.

Complete step-by-step answer:
The method of prime factorization is used to break down or express a given number as a product of prime numbers. More so, if a prime number occurs more than once in the factorization, it is usually expressed in exponential form to make it look more compact. Here, a prime number is a whole number greater than 1 that is only divisible by 1 and itself. Another way to say it is that a prime number has exactly two factors, namely 1 and itself. Let us explain prime factorization in steps.
First let us list down a few prime numbers: 2, 3, 5, 7, 11, 13, 17, etcetera.
Now, we have been asked to find the LCM of 12, 36 and 160.
Let us check again if the numbers are divisible by the prime number 2. After the repeated division of 2, you end up getting a prime number. Thus, we can form the prime factorization as,
$12=2\times 2\times 3$
$36=2\times 2\times 3\times 3$
$160=2\times 2\times 2\times 2\times 2\times 5$
Thus, to find the LCM from the above $\left( 2\times 2 \right)=4$ is common for the three numbers 12, 36 and 160.
Thus, we can write the LCM as (4 $\times $ the rest of the prime numbers)
$\therefore LCM=4\times 3\times 3\times 3\times 2\times 2\times 2\times 5=4320$
Thus, we got the LCM $=4320$ .

Note: We can also find the LCM using the division method.

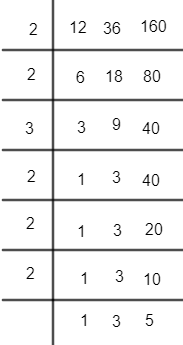
$\therefore LCM=2\times 2\times 3\times 3\times 2\times 2\times 2\times 3\times 5$
$={{2}^{5}}\times {{3}^{2}}\times 5=4320$