Question

find the LCM and HCF of the following integer by the prime factorization mass
A.12,15 and 21
B.17,23 and 29
C.8,9 and 25
D.72 and 108
E.72 and 108
F.306 and 657.

Answer 1

Hint: we will make use of the prime factorisation method.
The method of prime factorization is used to express a given number as a product of prime numbers. To find the prime factors we will see if the lowest number ,which is 2 , can divide the number whose prime factors we need to find out. If 2 cannot divide it then we proceed to 3 and so on.
To understand how to find prime factorisation we will take an example of how we will find the prime factorisation of 12.

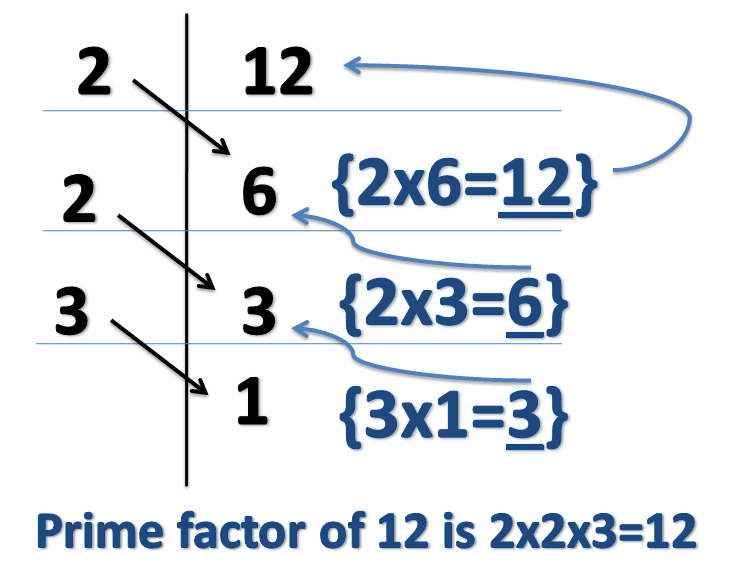
Prime factors of 12 are \[12=2\times 2\times 3\]



Complete step by step solution:
Prime factors of 12,15 and 21 are as follows:
Factors of \[12=2\times 2\times 3\]
Factors of \[15=3\times 5\]
Factors of \[21=3\times 7\]
HCF(highest common factor)=product of smallest power of each common prime factor.
\[\text{HCF=}{{\text{3}}^{1}}\] [since 3 is the only common factor in 12 ,15 and 21]
LCM(lowest common factor)=product of greatest power of each prime factor.
\[\text{LCM=}2\times 2\times 3\times 5\times 7=420\] [we don’t take 3 three times here because having 3 once is sufficient.]
\[\begin{gathered}
  & \text{LCM=}420 \\
 & \text{HCF=}{{\text{3}}^{1}} \\
\end{gathered}\]

Prime factors of 17,23 and 29 are as follows:
Factors of \[17=17\] [not divisible by any other factor or multiple]
Factors of \[23=23\]
Factors of \[29=29\]
\[\begin{gathered}
  & \text{LCM=17}\times 23\times 29=11339 \\
 & \text{HCF=Nothing} \\
\end{gathered}\][since there is not a single common factor between these three numbers].

Prime factors of 8,9 and 25 are as follows:
Factors of \[8=2\times 2\times 2\]
Factors of \[9=3\times 3\]
Factors of \[25=5\times 5\]
\[\begin{gathered}
  & \text{LCM=(2}\times 2\times 2)\times (3\times 3)\times (5\times 5)=1800 \\
 & \text{HCF=Nothing} \\
\end{gathered}\]

Prime factors of 72 and 108 are as follows:
Factors of \[72=2\times 2\times 2\times 3\times 3\]
Factors of \[108=2\times 2\times 3\times 3\times 3\]
\[\begin{gathered}
  & \text{LCM=(2}\times 2\times 2\times 3\times 3)\times (3)=216\text{ }\!\![\!\!\text{ we didnt take (2}\times 2\times 3\times 3)\text{from the factors of 108} \\
 & \text{ because they are already included in the factors of 72 }\!\!]\!\!\text{ } \\
 & \text{HCF=2}\times 2\times 3\times 3=36\text{ }\!\![\!\!\text{ only the common factors in between the two numbers }\!\!]\!\!\text{ } \\
\end{gathered}\]
Prime factors of 72 and 108 are as follows:
Factors of \[72=2\times 2\times 2\times 3\times 3\]
Factors of \[108=2\times 2\times 3\times 3\times 3\]
\[\begin{gathered}
  & \text{LCM=(2}\times 2\times 2\times 3\times 3)\times (3)=216\text{ }\!\![\!\!\text{ we didnt take (2}\times 2\times 3\times 3)\text{from the factors of 108} \\
 & \text{ because they are already included in the factors of 72 }\!\!]\!\!\text{ } \\
 & \text{HCF=2}\times 2\times 3\times 3=36\text{ }\!\![\!\!\text{ only the common factors in between the two numbers }\!\!]\!\!\text{ } \\
\end{gathered}\]
Prime factors of 306 and 657 are as follows:
Factors of \[306=2\times 3\times 3\times 17\]
Factors of \[657=3\times 3\times 73\]
\[\begin{gathered}
  & \text{LCM=(2}\times 3\times 3\times 17\times 73)=22338 \\
 & \text{HCF=}3\times 3=9 \\
\end{gathered}\]



Note:If a similar question comes then we need to first arrange the prime factors we found of each number properly and proceed with finding the H.C.F and L.C.M accordingly.

L.C.M is the least common multiple between the given number of terms. If there are no common multiples then those numbers itself will become the common multiple.
Example: the Least Common Multiple of 3 and 5 is 15
Because 15 is a multiple of 3 and also a multiple of 5 and it is the smallest number like that.
3 and 5 have other common multiples such as 30, 45, etc, but they are all larger than 15.