Question

Find the Lateral surface are (LSA), Total surface area (TSA) and volume of the cubes having their sides as:
(i). 5.6 cm
(ii). 6 dm
(iii). 2.5 m
(iv). 24 cm
(v). 31 cm

Answer 1

Hint: Cube is formed by the 6 faces in the form of squares. Total surface area of the cube is given as $6{{a}^{2}}$ and lateral surface area of the cube is $4{{a}^{2}}$ and volume of the cube is ${{\left( a \right)}^{3}}$, where a is the side of the cube of all the faces.

Complete Step-by-Step solution:
We know the cube is a 3-D geometrical structure with six equal squares i.e. all the sides involved (height, length, breadth) are the same. So, diagram of a cube is given as

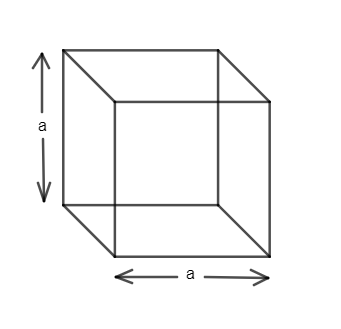
So, we can observe that there are six faces in the cube and hence the total surface area of the cube is the sum of areas of all the squares represented as faces. So, TSA (total surface area) is given as
TSA $=$ Area of six squares
We know Area of a square $=\left( side\times side \right)={{\left( side \right)}^{2}}$
Hence, we get
$TSA=6{{a}^{2}}$ ………………………………………..(i)
Now, we know the meaning of Lateral surface area as area of all the vertical faces. It means we need to ignore upper and lower faces for calculating the lateral or vertical surface area. So, we get
(Lateral Surface area) LSA $=$ Area of four squares
LSA $=4{{a}^{2}}$ ………………………………………(ii)
And we know Volume of any solid or hollow shape can be given by identity as
Volume $=$ Area of base $\times $ height
So, we have an area of base as ${{a}^{2}}$ and height be ‘a’. So, we get
Volume of cube $={{a}^{2}}\times a={{a}^{3}}$
Volume of cube $={{a}^{3}}$ ……………………………….(iii)
Now, come to the question:-

(i) Side $=5.6cm$
So, we can get TSA, LSA and volume from the equations (i), (ii) and (iii) respectively. So, put $a=5.6$ in each equation. So, we get
$TSA=6{{\left( 5.6 \right)}^{2}}$
$=188.16c{{m}^{2}}$
 LSA can be calculated as
LSA $=4{{a}^{2}}=4\times {{\left( 5.6 \right)}^{2}}$
$=125.44c{{m}^{2}}$
And hence, volume of cube can be given as
Volume $={{\left( 5.6 \right)}^{3}}=175.616c{{m}^{3}}$

(ii) Side $=6dm$
So, TSA can be calculated from equation (i) as
$TSA=6\times {{\left( 6 \right)}^{2}}$
$TSA=216d{{m}^{2}}$
And LSA can be given from equation (ii) as
$LSA=4\times {{\left( 6 \right)}^{2}}$
$LSA=144d{{m}^{2}}$
Now, we can get volume from the equation (iii) as
Volume $={{\left( 6 \right)}^{3}}$
$=216d{{m}^{3}}$

(iii) Side $=2.5m$
So, take $a=2.5m$
 TSA can be given from equation (i) as
$TSA=6\times {{\left( 2.5 \right)}^{2}}=37.5{{m}^{2}}$
LSA can be given from equation (ii) as
$LSA=4\times {{\left( 2.5 \right)}^{2}}$
$LSA=25{{m}^{2}}$
Volume will be calculated from the equation (iii) as
Volume $={{\left( 2.5 \right)}^{3}}$
$=15.625{{m}^{3}}$

(iv) Side $=24cm$
So, take $a=24cm$
TSA can be given from the equation (i) as
$TSA=6\times {{\left( 24 \right)}^{2}}$
$TSA=6\times 576=3456c{{m}^{2}}$
$TSA=3456c{{m}^{2}}$
 LSA can be given from equation (ii) as
$LSA=4\times {{\left( 24 \right)}^{2}}=4\times 576=2304c{{m}^{2}}$
$LSA=2304c{{m}^{2}}$
And volume can be given from equation (iii) as
Volume $={{\left( 24 \right)}^{3}}=12096c{{m}^{3}}$
Volume $=12096c{{m}^{3}}$

(v) Side $=31cm$
So, take $a=31cm$
And apply the relation in equation (i) to get TSA as
$TSA=6\times {{\left( 31 \right)}^{2}}=5766c{{m}^{2}}$
$TSA=5766c{{m}^{2}}$
LSA can be given from equation (ii) as
$LSA=4\times {{\left( 31 \right)}^{2}}=3844c{{m}^{2}}$
$LSA=3844c{{m}^{2}}$
And volume can be calculated from the equation (iii) as
Volume $={{\left( 31 \right)}^{3}}=29791c{{m}^{3}}$
Volume $=29791c{{m}^{3}}$

Note: Be clear with the total surface area and lateral surface area. One may go wrong if he/she uses the same formula for both or one may include any of the four faces or exclude any of the four faces of walls while writing the lateral surface area. So, don’t confuse the term Lateral surface area. Lateral means vertical, so we need to find the area of those faces only where height will come, so we do not need to consider upper and lower faces of the cube.
One should remember all those formulae derived in the question to solve the questions fastly. Use the unit very carefully. As units of side, and volume will differ and given as
Let unit of side $=m$
Then unit of area $={{m}^{2}}$
And unit of volume $={{m}^{3}}$
So, take care of units as well.