Question

Find the lateral and total surface area of the following pyramids.
(a) Square-based pyramid with base 6cm and slant height 14cm;
(b) Triangular-based pyramid with base 12 cm and slant height 20cm.

Answer 1

Hint: We are asked total surface area and curved surface area of the pyramid, we use formulas such as $ L.S.A=\dfrac{1}{2}P.l $ , and $ T.S.A=\dfrac{1}{2}P\times l+A $ .
Where,
‘P’ is the perimeter of the Base,
‘l’ is Slant height and
‘A’ denotes the area of the base.
We need an area of the square formula as $ {{\left( side \right)}^{2}} $ and the area of the base of the triangle as $ \dfrac{\sqrt{3}}{4}{{\left( side \right)}^{2}} $ .

Complete step by step answer:
We are asked to find the total and lateral surface area of the following pyramid.
We will find the following one by one.
(a) Square-based pyramid with base side is 6cm and slant height is 14cm.
As we know that ‘l’ is the lateral surface area we need the perimeter of the base and the slant height.
As we are given that our pyramid has a base as a square.

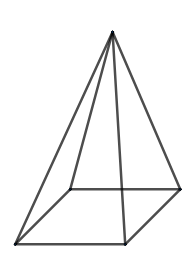
So,
The perimeter of the base of the pyramid (P) = the perimeter of the square.
Since the Side (s) of the square is 6.
So, its perimeter is $ 4\times S $
So, the Perimeter of square $ =4\times 6 $ ( as S=6)
=24
So, we get –
The perimeter of the pyramid base (P) =24.
Now, the lateral surface area of a pyramid with a square base is given as –
 $ L.S.A=\dfrac{1}{2}Pl $
Where,
P=24 and Slant height (l) = 14
So,
  $ \begin{align}
  & L.S.A=\dfrac{1}{2}\times 24\times 4 \\
 & L.S.A=168c{{m}^{2}} \\
\end{align} $
Now, the total surface area of a pyramid with a square base is given as –
 $ TSA=\dfrac{1}{2}Pl+A $
Where,
P=perimeter of the base, l=Slant height, and A= area of the base.
Since the square side is 6cm.
So, base area (A) – Area of square
 $ \begin{align}
  & =6\times 6 \\
 & =36c{{m}^{2}} \\
\end{align} $
Now using P=24, l=14, and A=36.
So we get –
 $ \begin{align}
  & TSA=\dfrac{1}{2}Pl+A \\
 & =\dfrac{1}{2}\times 24\times 14+36 \\
\end{align} $
By simplifying, we get –
 $ \begin{align}
  & =168+36 \\
 & =204c{{m}^{2}} \\
\end{align} $
So the total surface area of the pyramid is $ 204c{{m}^{2}} $ .
(b)
Now we have a pyramid with a triangular base.
So, for the lateral surface area, we first need the perimeter of the triangle.

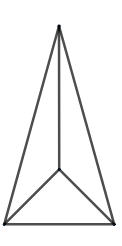
We have a side of the triangle that is 12cm
So, the perimeter of triangle $ \left( P \right)=3\times side $
 $ \begin{align}
  & =3\times 12 \\
 & =36cm \\
\end{align} $
Now, we have p=36cm and l=20cm
So, we find the lateral surface area using $ LSA=\dfrac{1}{2}Pl $
As p=36 and l=20 we get –
 $ =\dfrac{1}{2}\times 36\times 20 $
By simplifying we get –
 $ =360c{{m}^{2}} $
So, $ L.S.A=360c{{m}^{2}} $
So lateral surface area of the pyramid is $ 360c{{m}^{2}} $
Now for the total surface area, we need area as the total surface area is given as –
 $ T.S.A=\dfrac{1}{2}Pl+A $
Where ‘A’ is an area of the base
P = Perimeter if base
L = slant height.
The base is an equilateral triangle with a side of 12cm.
So, Area of Base = Area of an equilateral triangle
 $ =\dfrac{\sqrt{3}}{4}\times {{\left( side \right)}^{2}} $
As side = 12 cm
So, $ A=\dfrac{\sqrt{3}}{4}\times 12\times 12 $
By simplifying, we get –
 $ A=36\sqrt{3}c{{m}^{2}} $
Now using $ A=36\sqrt{3}c{{m}^{2}},\dfrac{1}{2}Pl=360 $ we get –
 $ \begin{align}
  & T.S.A=\dfrac{1}{2}Pl+A \\
 & =360+36\sqrt{3} \\
 & =36\left( 10+\sqrt{3} \right) \\
\end{align} $
So, we get –
The total surface area of a pyramid with a triangular base is $ 36\left( 10+\sqrt{3} \right) $

Note:
 The area is given as $ {{\left( side \right)}^{2}} $ for square common mistakes like $ {{6}^{2}}=12 $ happen were in the place of square one do the multiplication with 2. So, be clear there.
Remember –
 $ T.S.A=\dfrac{1}{2}Pl+A $ is neither but $ TSA=L.SA+A $
So, we do not have to solve $ \dfrac{1}{2}\times P\times l $ again.