
Find the largest number which divides 70 and 125 leaving remainder 5 and 8 respectively.
Answer
569.1k+ views
Hint:
We know that \[{\text{dividend = divisor}} \times {\text{quotient + remainder}}\] to find the two numbers that are completely divisible by the given divisors. Then, find the HCF of these two numbers for the required answer.
Complete step by step solution:
When 70 is divided by a number say $x$, it leaves the remainder 5.
That is,
$
{\text{70 = }}x \times {\text{quotient + 5}} \\
\Rightarrow 70 - 5 = x \times {\text{quotient}} \\
\Rightarrow 65 = x \times {\text{quotient}} \\
$
65 is completely divisible by the required number.
Similarly, $125 - 8 = 117$ is completely divisible by the required number.
Now, the required number is the HCF of 65 and 117.
Write the number 65 as the product of its primes.
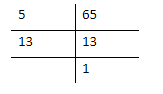
$65 = 5 \times 13$
Similarly, write the number 117 as the product of its primes.
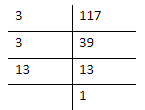
$117 = 3 \times 3 \times 13$
Therefore, the HCF is 13
Thus, the largest number which divides 70 and 125 leaving remainder 5 and 8 respectively is 13.
Note:
We can also calculate the HCF by long division method or factor tree method. HCF of numbers gives the largest number that divides all the given numbers.
We know that \[{\text{dividend = divisor}} \times {\text{quotient + remainder}}\] to find the two numbers that are completely divisible by the given divisors. Then, find the HCF of these two numbers for the required answer.
Complete step by step solution:
When 70 is divided by a number say $x$, it leaves the remainder 5.
That is,
$
{\text{70 = }}x \times {\text{quotient + 5}} \\
\Rightarrow 70 - 5 = x \times {\text{quotient}} \\
\Rightarrow 65 = x \times {\text{quotient}} \\
$
65 is completely divisible by the required number.
Similarly, $125 - 8 = 117$ is completely divisible by the required number.
Now, the required number is the HCF of 65 and 117.
Write the number 65 as the product of its primes.
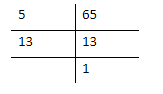
$65 = 5 \times 13$
Similarly, write the number 117 as the product of its primes.

$117 = 3 \times 3 \times 13$
Therefore, the HCF is 13
Thus, the largest number which divides 70 and 125 leaving remainder 5 and 8 respectively is 13.
Note:
We can also calculate the HCF by long division method or factor tree method. HCF of numbers gives the largest number that divides all the given numbers.
Recently Updated Pages
Master Class 8 Social Science: Engaging Questions & Answers for Success

Master Class 8 Maths: Engaging Questions & Answers for Success

Master Class 8 Science: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 English: Engaging Questions & Answers for Success

Why are manures considered better than fertilizers class 11 biology CBSE

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Citizens of India can vote at the age of A 18 years class 8 social science CBSE

Full form of STD, ISD and PCO

Right to vote is a AFundamental Right BFundamental class 8 social science CBSE

What is the difference between rai and mustard see class 8 biology CBSE

Summary of the poem Where the Mind is Without Fear class 8 english CBSE





