Question

How do you find the inverse of $f(x)=2x-3$, and graph both $f$and \[{{f}^{-1}}\]

Answer 1

Hint: We are given $f(x)=2x-3$, to find the inverse of the function, we first learn what does inverse implies. We will follow a step by step method to find the inverse once we have the inverse, we will find the coordinate. That lie on \[f(x)\]and also \[{{f}^{-1}}(x)\] with their coordinates. We put them on the graph and sketch the graph of our required functions. We will use an algebraic tool to simplify and evaluate our inverse of \[f(x)\].

Complete step by step answer:
We are given the function \[f(x)\] which is defined as $f(x)=2x-3$. We are asked to find the inverse of this function and we also have to sketch these on graph
Now we first learn what the inverse of a function means, then we will learn how to find the inverse for any function say \[g(x)\]. The inverse of the function is another function such that the composition of these two functions will become an identity function.
That if \[{{g}^{-1}}(x)\] denote inverse of \[g(x)\]Then
\[\begin{align}
  & g\left( {{g}^{-1}}\left( x \right) \right)=x \\
 & {{g}^{-1}}\left( g\left( x \right) \right)=x \\
\end{align}\]
Now to find the inverse of any function we follow these steps:
1. Replace the function \[f(x)\] by y.
2. now change all x as y and all y as x
3. now solve to find the value of y.
Simplify,
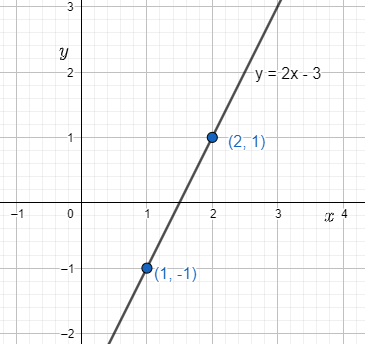
For $x=2$we have
$\begin{align}
  & f(x)=2\times 2-3 \\
 & =1 \\
\end{align}$
so, for $x=2$ we have $y=1$
so, we get
\[\left( 1,-1 \right)\,\operatorname{and}\,\left( 2,+1 \right)\] lie of $f(x)=2x-3$
We put them on graphs and sketches.

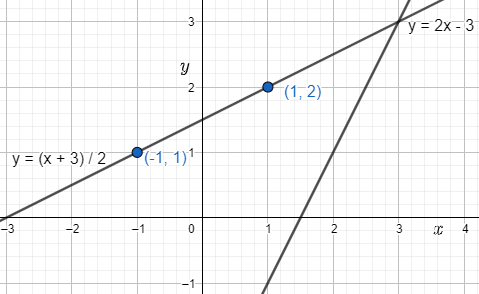
Similarly, we find value of point lie on ${{f}^{-1}}(x)=\dfrac{x+3}{2}$
When \[x=1\], we have \[{{f}^{-1}}(1)=\dfrac{1+3}{2}=2\]
So, for \[x=1\], we have \[y=2\] for \[{{f}^{-1}}(x)\]
When \[x=1\], we have \[{{f}^{-1}}(1)=\dfrac{1+3}{2}=\dfrac{2}{2}=1\]
So, for \[x=-1\], we have \[y=1\] for \[{{f}^{-1}}(x)\]
So we get \[(1,2)\] and \[(-1,1)\] lie on \[{{f}^{-1}}(x)=\dfrac{x+3}{2}\]
So, putting on graph

Note:
When we sketch the graph of \[f(x)\] and it’s inverse on the same axis then the graph of \[{{f}^{-1}}(x)\] in the mirror reflection of \[f(x)\] with respect to the \[y=x\] find the graph of and its inverse in some as like reflection of us into a mirror. It is also the test to check whether a graph drawn is correct or not.