
Find the interval in which the function given by \[f\left( x \right) = \dfrac{3}{10}x^{4} - \dfrac{4}{5}x^{3} – 3x^{2} + \dfrac{36}{5}x + 11\ \] is
A. Strictly increasing
B. Strictly decreasing
Answer
480.6k+ views
Hint: In this question, we need to find the interval of the given expression \[f\left( x \right) = \dfrac{3}{10}x^{4} - \dfrac{4}{5}x^{3} – 3x^{2} + \dfrac{36}{5}x + 11\ \] and need to conclude that the interval of the expression is increasing or decreasing. First, we need to find the differentiation of \[f(x)\] that is \[f’(x)\]. Then we check \[f’(x) = 0\] . Using this we can find the value of \[x\] and then we need to plot the value of \[x\] in a number , in order to find the interval of \[f(x)\] .
Complete answer:
Given,
\[f\left( x \right) = \dfrac{3}{10}x^{4} - \dfrac{4}{5}x^{3} – 3x^{2} + \dfrac{36}{5}x + 11\]
First let us differentiate the given expression \[f(x)\] .
That is \[f’\left( x \right) = \dfrac{3}{10}\left( 4x^{3} \right) - \dfrac{4}{5}\left( 3x^{2} \right) – 3\left( 2x \right) + \dfrac{36}{5} + 0\]
On simplifying,
We get ,
\[\Rightarrow \ f^{‘}\left( x \right) = \dfrac{6}{5}x^{3} - \dfrac{12}{5}x^{2} – 6x + \dfrac{36}{5}\]
Now on taking LCM,
We get
\[\Rightarrow \ f’(x) = \left( \dfrac{6x^{3} – 12x^{2} – 30x + 36}{5} \right)\]
On taking 6 common,
We get ,
\[\Rightarrow \ f’\left( x \right) = \dfrac{6}{5}\left( x^{3} – 2x^{2} – 5x + 6 \right)\]
Now on splitting the terms in parentheses,
We get
\[\Rightarrow \ f’\left( x \right) = \dfrac{6}{5}\left( x^{3} – x^{2} – x^{2} + x – 6x + 6 \right)\]
Now on taking \[(x – 1)\] common,
We get,
\[\Rightarrow \ f’\left( x \right) = \dfrac{6}{5}\left( x^{2}\left( x – 1 \right) – x\left( x – 1 \right) – 6\left( x – 1 \right) \right)\]
Thus we get,
\[\Rightarrow \ f’\left( x \right) = \dfrac{6}{5}\left( \left( x – 1 \right)\left( x^{2} – x – 6 \right) \right)\]
Again on factoring the term \[\left( x^{2} – x – 6 \right)\]
We get,
\[\Rightarrow \ f’\left( x \right) = \dfrac{6}{5}\left( \left( x – 1 \right)\left( x + 2 \right)\left( x – 3 \right) \right)\]
On putting \[f’(x)\ = 0\] ,
We get,
\[\dfrac{6}{5}\left( \left( x – 1 \right)\left( x + 2 \right)\left( x – 3 \right) \right) = 0\]
Now on multiplying both sides by \[\dfrac{5}{6}\],
We get,
\[\left( \left( x – 1 \right)\left( x + 2 \right)\left( x – 3 \right) \right) = 0\]
Here \[x = 1,\ - 2,\ 3\]
Now let us point the values of \[x\] in a number line.
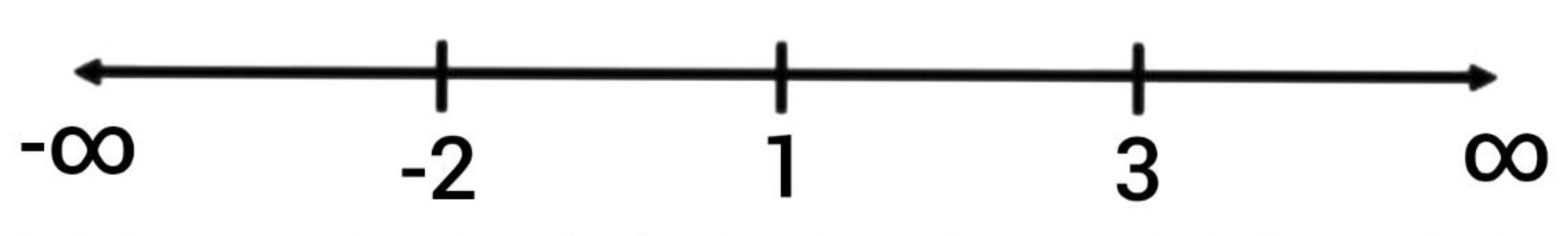
Hence \[f(x)\] is strictly increasing in the interval \[( - 2,\ 1)\] and \[(3,\ \infty)\]
And \[f(x)\] is strictly decreasing in the interval of \[( - \infty,\ - 2)\] and \[(1,\ 3)\]
Final answer :
A. \[f(x)\] is strictly increasing in the interval \[( - 2,\ 1)\] and \[(3,\ \infty)\]
B. \[f(x)\] is strictly decreasing in the interval of \[( - \infty,\ - 2)\] and \[(1,\ 3)\]
Note: In order to solve these types of questions, we should have a strong grip over strictly increasing and decreasing functions. We also need to know that a function is said to increase when the y-value increases as the x-value increases similarly, a function is said to be decreasing when the x-value increases as the y-value increases. We should be very careful , while splitting the intervals of the function.
Complete answer:
Given,
\[f\left( x \right) = \dfrac{3}{10}x^{4} - \dfrac{4}{5}x^{3} – 3x^{2} + \dfrac{36}{5}x + 11\]
First let us differentiate the given expression \[f(x)\] .
That is \[f’\left( x \right) = \dfrac{3}{10}\left( 4x^{3} \right) - \dfrac{4}{5}\left( 3x^{2} \right) – 3\left( 2x \right) + \dfrac{36}{5} + 0\]
On simplifying,
We get ,
\[\Rightarrow \ f^{‘}\left( x \right) = \dfrac{6}{5}x^{3} - \dfrac{12}{5}x^{2} – 6x + \dfrac{36}{5}\]
Now on taking LCM,
We get
\[\Rightarrow \ f’(x) = \left( \dfrac{6x^{3} – 12x^{2} – 30x + 36}{5} \right)\]
On taking 6 common,
We get ,
\[\Rightarrow \ f’\left( x \right) = \dfrac{6}{5}\left( x^{3} – 2x^{2} – 5x + 6 \right)\]
Now on splitting the terms in parentheses,
We get
\[\Rightarrow \ f’\left( x \right) = \dfrac{6}{5}\left( x^{3} – x^{2} – x^{2} + x – 6x + 6 \right)\]
Now on taking \[(x – 1)\] common,
We get,
\[\Rightarrow \ f’\left( x \right) = \dfrac{6}{5}\left( x^{2}\left( x – 1 \right) – x\left( x – 1 \right) – 6\left( x – 1 \right) \right)\]
Thus we get,
\[\Rightarrow \ f’\left( x \right) = \dfrac{6}{5}\left( \left( x – 1 \right)\left( x^{2} – x – 6 \right) \right)\]
Again on factoring the term \[\left( x^{2} – x – 6 \right)\]
We get,
\[\Rightarrow \ f’\left( x \right) = \dfrac{6}{5}\left( \left( x – 1 \right)\left( x + 2 \right)\left( x – 3 \right) \right)\]
On putting \[f’(x)\ = 0\] ,
We get,
\[\dfrac{6}{5}\left( \left( x – 1 \right)\left( x + 2 \right)\left( x – 3 \right) \right) = 0\]
Now on multiplying both sides by \[\dfrac{5}{6}\],
We get,
\[\left( \left( x – 1 \right)\left( x + 2 \right)\left( x – 3 \right) \right) = 0\]
Here \[x = 1,\ - 2,\ 3\]
Now let us point the values of \[x\] in a number line.
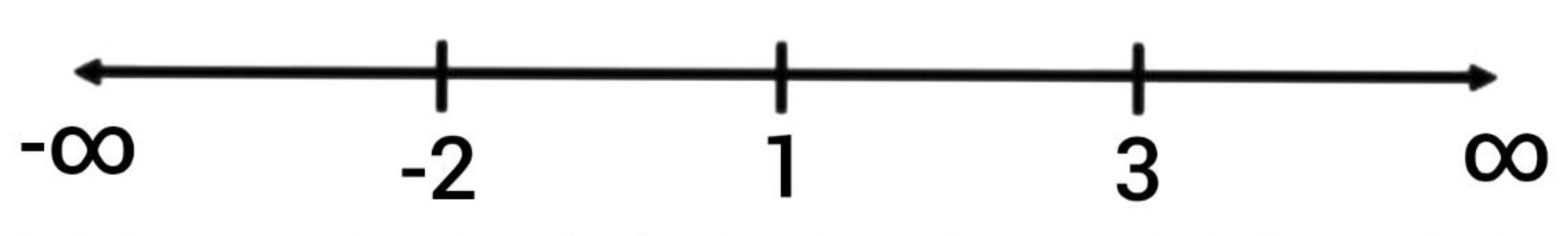
| Values of \[x\] | Intervals | Sign of \[f’(x) = 0\] | Nature of \[f(x) \] |
| \[- \infty < x < - 2\] | \[( - \infty,\ - 2)\] | \[( - )( - )( - )\ < 0\] | Strictly decreasing |
| \[- 2 < x < 1\] | \[( - 2,\ 1)\] | \[( - )( + )( - ) > 0\] | Strictly increasing |
| \[1 < x < 3\] | \[(1,\ 3)\] | \[( + )( + )( - )\ < 0\] | Strictly decreasing |
| \[3 < x < \infty\] | \[(3,\ \infty)\] | \[( + )( + )( + ) > 0\] | Strictly increasing |
Hence \[f(x)\] is strictly increasing in the interval \[( - 2,\ 1)\] and \[(3,\ \infty)\]
And \[f(x)\] is strictly decreasing in the interval of \[( - \infty,\ - 2)\] and \[(1,\ 3)\]
Final answer :
A. \[f(x)\] is strictly increasing in the interval \[( - 2,\ 1)\] and \[(3,\ \infty)\]
B. \[f(x)\] is strictly decreasing in the interval of \[( - \infty,\ - 2)\] and \[(1,\ 3)\]
Note: In order to solve these types of questions, we should have a strong grip over strictly increasing and decreasing functions. We also need to know that a function is said to increase when the y-value increases as the x-value increases similarly, a function is said to be decreasing when the x-value increases as the y-value increases. We should be very careful , while splitting the intervals of the function.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




