
Find the interval for which the function $f\left( x \right)=\dfrac{\left| x-1 \right|}{{{x}^{2}}}$ is monotonically decreasing. \[\]
Answer
555.6k+ views
Hint: We find the critical points of the function by finding where ${{f}^{'}}\left( x \right)$ is either not defined or ${{f}^{'}}\left( x \right)=0$. We divide the real number set into subintervals using those critical points. We check in which interval ${{f}^{'}}\left( x \right)\le 0$ and that interval we use the fact that a monotonically decreasing function in $\left[ a,b \right]$will have ${{f}^{'}}\left( x \right)\le 0$ for all $x\in \left[ a,b \right]$.\[\]
Complete step by step answer:
We know that the monotonically decreasing function in $\left[ a,b \right]$will have the first derivative${{f}^{'}}\left( x \right)\le 0$ for all $x\in \left[ a,b \right]$. We cannot say anything about the monotonicity at the points where $f\left( x \right)$ is not defined. The values for which the derivative vanishes or is not defined are called critical points and the function changes its monotonicity at critical points. \[\]
We know that absolute value function is defined as follows.
\[f\left( x \right)=\left\{ \begin{matrix}
x & \text{if }x\ge 0 \\
-x & \text{if }x<0 \\
\end{matrix} \right.\]
We see that functions always return positive value and is piecewise defined at $x=0$.We are given the following function in the question
\[f\left( x \right)=\dfrac{\left| x-1 \right|}{{{x}^{2}}}\]
We see that function is defined at $x=0$ since denominator cannot be zero. Hence $x=0$ is a critical point. We see that numerator has absolute value function and piecewise defined at$x=1$. We know that the derivative of absolute value function does not exist at point for piecewise definition, which means ${{f}^{'}}\left( x \right)$ does not exist.
Case-1: If we have $x<1$ then $\left| x-1 \right|=-\left( x-1 \right)=1-x$ since absolsute function must return positive value and the function has the following definition:
\[\begin{align}
& f\left( x \right)=\dfrac{1-x}{{{x}^{2}}} \\
& \Rightarrow f\left( x \right)=\dfrac{1}{{{x}^{2}}}-\dfrac{x}{{{x}^{2}}} \\
& \Rightarrow f\left( x \right)=\dfrac{1}{{{x}^{2}}}-\dfrac{1}{x} \\
\end{align}\]
Let us differentiate the above function with respect to $x$ and have;
\[\begin{align}
& {{f}^{'}}\left( x \right)=-\dfrac{2}{{{x}^{3}}}+\dfrac{1}{{{x}^{2}}} \\
& \Rightarrow {{f}^{'}}\left( x \right)=\dfrac{x-2}{{{x}^{3}}} \\
\end{align}\]
We see that ${{f}^{'}}\left( x \right)=0$ at $x=2$ which makes $x=2$ a critical point. \[\]
Case-2: If we have $x\ge 1$ then $\left| x-1 \right|=x-1$ since absolute function must return positive value and the function has the following definition:
\[\begin{align}
& f\left( x \right)=\dfrac{x-1}{{{x}^{2}}} \\
& \Rightarrow f\left( x \right)=\dfrac{x}{{{x}^{2}}}-\dfrac{1}{{{x}^{2}}} \\
& \Rightarrow {{f}^{'}}\left( x \right)=\dfrac{1}{x}-\dfrac{1}{{{x}^{2}}} \\
\end{align}\]
Let us differentiate the above function with respect to $x$ and have;
\[\begin{align}
& {{f}^{'}}\left( x \right)=-\dfrac{1}{{{x}^{2}}}+\dfrac{2}{{{x}^{3}}} \\
& \Rightarrow {{f}^{'}}\left( x \right)=\dfrac{2-x}{{{x}^{3}}} \\
\end{align}\]
We again see that ${{f}^{'}}\left( x \right)=0$ at $x=2$ which gives the same critical point $x=0$. So we have the critical points $0,1,2$. We use the wavy curve method to check for which intervals in $\mathsf{\mathbb{R}}$, we have ${{f}^{'}}\left( x \right)\le 0$.
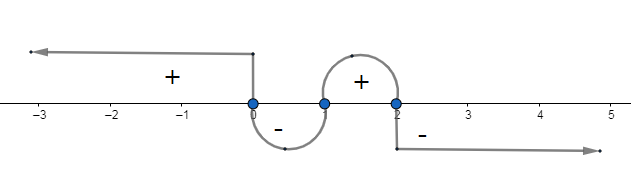
We see that ${{f}^{'}}\left( x \right)\le 0$ for $x\in \left( 0,1 \right)$ and $\left[ 2,\infty \right)$. So the function is monotonically decreasing in $\left( 0,1 \right)\bigcup \left[ 2,\infty \right)$. \[\]
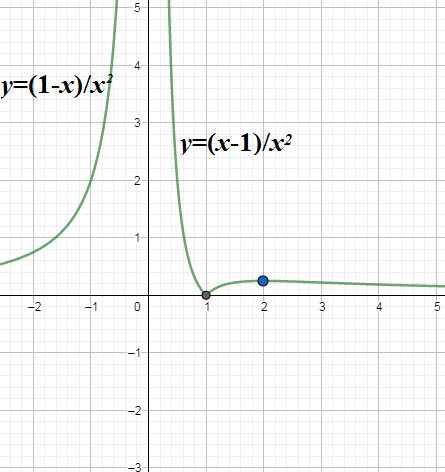
Note: We can alternatively use quotient rule $\dfrac{d}{dx}\left( \dfrac{u}{v} \right)=\dfrac{u{{v}^{'}}-{{u}^{'}}v}{{{v}^{2}}}$ to differentiate the functions. We must be careful that the absolute value function does not have derivative at $x=0$ but is continuous at $x=0$. We say the function is strictly decreasing if ${{f}^{'}}\left( x \right)<0$. If ${{f}^{'}}\left( a \right)=0$ for some $x=a$ and if we see that the function is still decreasing or increasing we call ,$x=a$ a point of inflection.
Complete step by step answer:
We know that the monotonically decreasing function in $\left[ a,b \right]$will have the first derivative${{f}^{'}}\left( x \right)\le 0$ for all $x\in \left[ a,b \right]$. We cannot say anything about the monotonicity at the points where $f\left( x \right)$ is not defined. The values for which the derivative vanishes or is not defined are called critical points and the function changes its monotonicity at critical points. \[\]
We know that absolute value function is defined as follows.
\[f\left( x \right)=\left\{ \begin{matrix}
x & \text{if }x\ge 0 \\
-x & \text{if }x<0 \\
\end{matrix} \right.\]
We see that functions always return positive value and is piecewise defined at $x=0$.We are given the following function in the question
\[f\left( x \right)=\dfrac{\left| x-1 \right|}{{{x}^{2}}}\]
We see that function is defined at $x=0$ since denominator cannot be zero. Hence $x=0$ is a critical point. We see that numerator has absolute value function and piecewise defined at$x=1$. We know that the derivative of absolute value function does not exist at point for piecewise definition, which means ${{f}^{'}}\left( x \right)$ does not exist.
Case-1: If we have $x<1$ then $\left| x-1 \right|=-\left( x-1 \right)=1-x$ since absolsute function must return positive value and the function has the following definition:
\[\begin{align}
& f\left( x \right)=\dfrac{1-x}{{{x}^{2}}} \\
& \Rightarrow f\left( x \right)=\dfrac{1}{{{x}^{2}}}-\dfrac{x}{{{x}^{2}}} \\
& \Rightarrow f\left( x \right)=\dfrac{1}{{{x}^{2}}}-\dfrac{1}{x} \\
\end{align}\]
Let us differentiate the above function with respect to $x$ and have;
\[\begin{align}
& {{f}^{'}}\left( x \right)=-\dfrac{2}{{{x}^{3}}}+\dfrac{1}{{{x}^{2}}} \\
& \Rightarrow {{f}^{'}}\left( x \right)=\dfrac{x-2}{{{x}^{3}}} \\
\end{align}\]
We see that ${{f}^{'}}\left( x \right)=0$ at $x=2$ which makes $x=2$ a critical point. \[\]
Case-2: If we have $x\ge 1$ then $\left| x-1 \right|=x-1$ since absolute function must return positive value and the function has the following definition:
\[\begin{align}
& f\left( x \right)=\dfrac{x-1}{{{x}^{2}}} \\
& \Rightarrow f\left( x \right)=\dfrac{x}{{{x}^{2}}}-\dfrac{1}{{{x}^{2}}} \\
& \Rightarrow {{f}^{'}}\left( x \right)=\dfrac{1}{x}-\dfrac{1}{{{x}^{2}}} \\
\end{align}\]
Let us differentiate the above function with respect to $x$ and have;
\[\begin{align}
& {{f}^{'}}\left( x \right)=-\dfrac{1}{{{x}^{2}}}+\dfrac{2}{{{x}^{3}}} \\
& \Rightarrow {{f}^{'}}\left( x \right)=\dfrac{2-x}{{{x}^{3}}} \\
\end{align}\]
We again see that ${{f}^{'}}\left( x \right)=0$ at $x=2$ which gives the same critical point $x=0$. So we have the critical points $0,1,2$. We use the wavy curve method to check for which intervals in $\mathsf{\mathbb{R}}$, we have ${{f}^{'}}\left( x \right)\le 0$.

We see that ${{f}^{'}}\left( x \right)\le 0$ for $x\in \left( 0,1 \right)$ and $\left[ 2,\infty \right)$. So the function is monotonically decreasing in $\left( 0,1 \right)\bigcup \left[ 2,\infty \right)$. \[\]
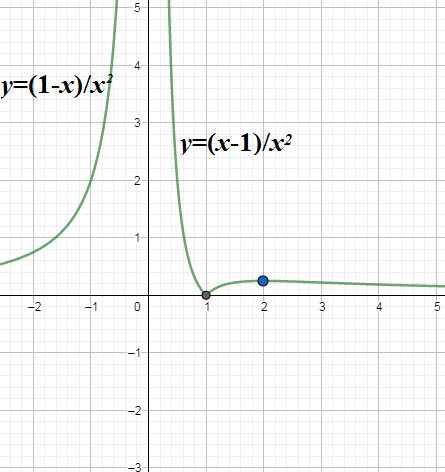
Note: We can alternatively use quotient rule $\dfrac{d}{dx}\left( \dfrac{u}{v} \right)=\dfrac{u{{v}^{'}}-{{u}^{'}}v}{{{v}^{2}}}$ to differentiate the functions. We must be careful that the absolute value function does not have derivative at $x=0$ but is continuous at $x=0$. We say the function is strictly decreasing if ${{f}^{'}}\left( x \right)<0$. If ${{f}^{'}}\left( a \right)=0$ for some $x=a$ and if we see that the function is still decreasing or increasing we call ,$x=a$ a point of inflection.
Recently Updated Pages
Basicity of sulphurous acid and sulphuric acid are

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Trending doubts
What are the major means of transport Explain each class 12 social science CBSE

Which are the Top 10 Largest Countries of the World?

Draw a labelled sketch of the human eye class 12 physics CBSE

How much time does it take to bleed after eating p class 12 biology CBSE

Explain sex determination in humans with line diag class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE




