Question

How do you find the intercepts, extrema, points of inflections, asymptotes and graph $ y=\dfrac{20x}{{{x}^{2}}+1}-\dfrac{1}{x} $ ?

Answer 1

Hint: We first find the intercepts from the points $ x=0 $ and $ y=0 $ . Then we find the second derivative and the graph to find the extrema and points of inflections. We also check the asymptotes taking the characteristics of the curve at $ x\to \pm \infty $ .

Complete step-by-step answer:
We have to find the intercepts, extrema, points of inflections, asymptotes, graph of $ y=\dfrac{20x}{{{x}^{2}}+1}-\dfrac{1}{x} $ .
The simplified form is $ y=\dfrac{20x}{{{x}^{2}}+1}-\dfrac{1}{x}=\dfrac{19{{x}^{2}}-1}{x\left( {{x}^{2}}+1 \right)} $ .
We have to find the possible number of x intercepts and the value of the y intercept. The curve cuts the X and Y axis at certain points and those are the intercepts.
We first find the Y-axis intercepts. In that case for the Y-axis, we have to take the coordinate values of x as 0. Putting the value of $ x=0 $ in the equation $ y=\dfrac{20x}{{{x}^{2}}+1}-\dfrac{1}{x} $ .
But the function is not defined at $ x=0 $ . It has no Y-axis intercepts.
We find the X-axis intercepts. In that case for X-axis, we have to take the coordinate values of y as 0. Putting the value of $ y=0 $ in the equation $ y=\dfrac{19{{x}^{2}}-1}{x\left( {{x}^{2}}+1 \right)} $ , we get
\[\begin{align}
  & y=\dfrac{19{{x}^{2}}-1}{x\left( {{x}^{2}}+1 \right)} \\
 & \Rightarrow 0=\dfrac{19{{x}^{2}}-1}{x\left( {{x}^{2}}+1 \right)} \\
 & \Rightarrow 19{{x}^{2}}=1 \\
 & \Rightarrow x=\pm \sqrt{\dfrac{1}{19}} \\
\end{align}\]
The intercept point for X-axis is $ \left( \pm \sqrt{\dfrac{1}{19}},0 \right) $ . There are two intercepts for X-axis.
For vertical asymptotes we have to find the denominator of $ y=\dfrac{19{{x}^{2}}-1}{x\left( {{x}^{2}}+1 \right)} $ equal to 0.
So, $ x\left( {{x}^{2}}+1 \right)=0 $ gives $ x=0 $ . The curve has vertical asymptotes at $ x=0 $ and that’s why it has no Y-axis intercepts.
For horizontal asymptotes we examine the curve $ y=\dfrac{19{{x}^{2}}-1}{x\left( {{x}^{2}}+1 \right)} $ at $ x\to \pm \infty $ .
 $ y=\dfrac{19{{x}^{2}}-1}{x\left( {{x}^{2}}+1 \right)}=\dfrac{19}{\left( x+\dfrac{1}{x} \right)}-\dfrac{1}{x\left( {{x}^{2}}+1 \right)} $ .
As $ x\to \pm \infty $ , $ y=\dfrac{19}{\left( x+\dfrac{1}{x} \right)}-\dfrac{1}{x\left( {{x}^{2}}+1 \right)}\to 0 $ . Therefore, it has horizontal asymptotes along the X-axis as $ x\to \pm \infty $ .
For extremums we find derivatives of $ y=\dfrac{19{{x}^{2}}-1}{x\left( {{x}^{2}}+1 \right)} $ .
We have $ {{y}^{'}}=\dfrac{38{{x}^{2}}\left( {{x}^{2}}+1 \right)-\left( 19{{x}^{2}}-1 \right)\left( 3{{x}^{2}}+1 \right)}{{{x}^{2}}{{\left( {{x}^{2}}+1 \right)}^{2}}}=-\dfrac{19{{x}^{4}}-22{{x}^{2}}-1}{{{x}^{2}}{{\left( {{x}^{2}}+1 \right)}^{2}}} $ .
Equating with 0 we get $ 19{{x}^{4}}-22{{x}^{2}}-1=0 $ .
The solution of the quadratic gives $ x=\pm 1.096 $ .
We now draw the graph to find the extrema and points of inflections.

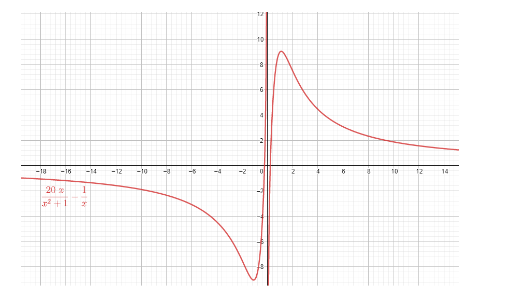
Near the points $ x=\pm 1.096 $ , we have the critical points of $ y=\pm 9.046 $ .
Those are also the inflection points as the curve changes its concavity, from being "concave up" to being "concave down" or vice versa.

Note: We need to remember the concept of extremum and point of inflection is quite similar. The slopes decide the concavity and its change. We also need to remember that If a function is undefined at some value of x, there can be no inflection point.