Question

How do you find the inscribed circle in a triangle?

Answer 1

Hint: We first explain the terms incircle, incentre and inradius. Then we draw a whole diagram and explain the incircle through the diagram. We use the angle bisector and perpendicular distance formula to find the radius and draw the incircle.

Complete answer:
We first explain the terms incircle, incentre and inradius. The intersecting point of all the angle bisectors of a triangle is called the incentre of that triangle. Then we take the perpendicular distance from the incentre to any one of the sides of the triangle and draw a circle with that value which becomes the incircle of the triangle. The radius of the circle is called the inradius of the triangle.
We now draw a triangle whose sides measures are $a,b,c$ units. Then we draw its incircle. $\Delta ABC$ is the triangle, O is the incentre and the inradii are $OD=OE=OF=r$.

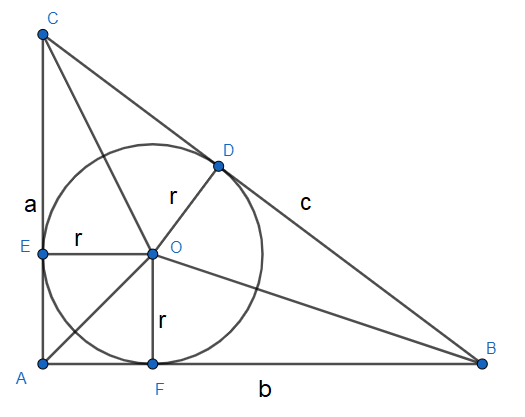
First, we find the three angle bisectors of the angles $\angle A,\angle B,\angle C$. Those bisectors intersect each other at O. This is the incentive of the $\Delta ABC$. Now we take the perpendicular distance from O to any one side of the triangle. We take the perpendicular length and use it as the radius to draw the incircle. The circle will touch each side at a fixed point which is the base point of the perpendicular distance. Therefore, we use $OD=r$ and get the incircle.

Note:
The inradius can be found for any side as they will be similar for the incircle. The difference of incircle from the circumcircle is that in circumcircle, we first find the intersection point of three perpendicular bisectors of the sides and then take the distance from a vertex as the circumradius.