Question

How do you find the inflection point of the function $f\left( x \right)=x{{e}^{-2x}}$? \[\]

Answer 1

Hint: We recall the point of inflection of curve corresponding function which is obtained as the solutions of ${{f}^{''}}\left( x \right)=0$. We differentiate the given function $f\left( x \right)=x{{e}^{-2x}}$ two times with respect to $x$ and then equate to zero . We solve for $x$ to get the point of inflection. \[\]

Complete step-by-step answer:
We know while the second derivative of any function $f\left( x \right)$ at any point $x=p$ represents the concavity of the curve of $f\left( x \right)$ at $x=p$. If the second derivative ${{f}^{''}}\left( p \right) > 0$ then curve of $f\left( x \right)$ is concave upward at $x=p$ and if ${{f}^{''}}\left( p \right) < 0$ then the curve of $f\left( x \right)$ is concave downward at $x=p$. If ${{f}^{''}}\left( p \right)=0$ then we call $x=p$ the point of inflection because at this point graph of $f\left( x \right)$ changes its shape from concave upward to concave downward or vice-versa. The second derivative ${{f}^{''}}\left( x \right)$ changes its sign from positive to negative or vice-versa.\[\]
We are given the following function in the question
\[f\left( x \right)=x{{e}^{-2x}}\]
Let us differentiate the above function with respect to $x$ using product rule to have the first derivative as ;
\[\begin{align}
  & {{f}^{'}}\left( x \right)=\dfrac{d}{dx}\left( x{{e}^{-2x}} \right) \\
 & \Rightarrow {{f}^{'}}\left( x \right)=x\cdot \left( -2 \right){{e}^{-2x}}+{{e}^{-2x}}\cdot 1 \\
 & \Rightarrow {{f}^{'}}\left( x \right)=-2x{{e}^{-2x}}+{{e}^{-2x}} \\
 & \Rightarrow {{f}^{'}}\left( x \right)={{e}^{-2x}}\left( 1-2x \right) \\
\end{align}\]
We differentiate the above function again with respect to $x$ using product rule to have the second derivative as;
\[\begin{align}
  & \Rightarrow {{f}^{''}}\left( x \right)=\dfrac{d}{dx}\left( {{e}^{-2x}}\left( 1-2x \right) \right) \\
 & \Rightarrow {{f}^{''}}\left( x \right)={{e}^{-2x}}\cdot \left( -2 \right)+\left( 1-2x \right)\left( -2 \right)\cdot {{e}^{-2x}} \\
 & \Rightarrow {{f}^{''}}\left( x \right)={{e}^{-2x}}\left( -2-2+4x \right) \\
 & \Rightarrow {{f}^{''}}\left( x \right)={{e}^{-2x}}\left( 4x-4 \right) \\
\end{align}\]
Let us equate the second derivative to zero to find the inflection point
\[\begin{align}
  & \Rightarrow {{f}^{''}}\left( x \right)=0 \\
 & \Rightarrow {{e}^{-2x}}\left( 4x-4 \right)=0 \\
 & \Rightarrow 4x-4=0\left( \because {{e}^{-2x}}\ne 0\forall x \right) \\
 & \Rightarrow x=1 \\
\end{align}\]
So the point of inflection is $x=1$.
We can check whether the ${{f}^{''}}\left( x \right)$ changes its sign at $x=1$. We take $x=0$ at the left of $x=1$ to find ${{f}^{''}}\left( 0 \right)={{e}^{-2\cdot 0}}\left( 4\cdot 0-4 \right)=-4 < 0$ and we take $x=2$ at the right of $x=1$ find ${{f}^{''}}\left( 0 \right)={{e}^{-2\cdot 1}}\left( 4\cdot 2-4 \right)=\dfrac{4}{{{e}^{2}}} > 0$. So $x=1$ is verified to be point of inflection which in the graph is $\left( 1,\dfrac{1}{{{e}^{2}}} \right)$.\[\]

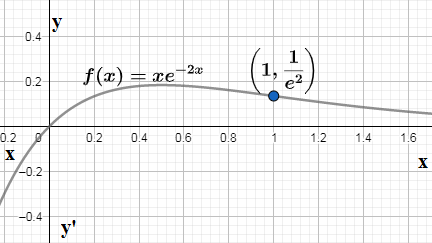
Note: We note that just like second derivative determines the nature of concavity at $x=p$ then the first derivative ${{f}^{'}}\left( x \right)$ determines the nature of slope of tangent at $x=p$ $\left( 1,\dfrac{1}{{{e}^{2}}} \right)$ . We also note that the inflection is different from point of maxima or minima which in this case is at $x=0.5$ and $f\left( x \right)=\dfrac{1}{2e}$ where first derivative ${{f}^{'}}\left( x \right)$ changes its sign.