Question

How do find the inflection point, concave up and concave down for
$f(x) = {x^3} - 3{x^2} + 3$

Answer 1

Hint: Second derivation of any kind of graph function shows inflection point.
When we do a second derivation of the graph function to see for the change in the concavity nature of the graph like change from concave up to concave down or vice versa. The point at which the change starts is called the inflection point.

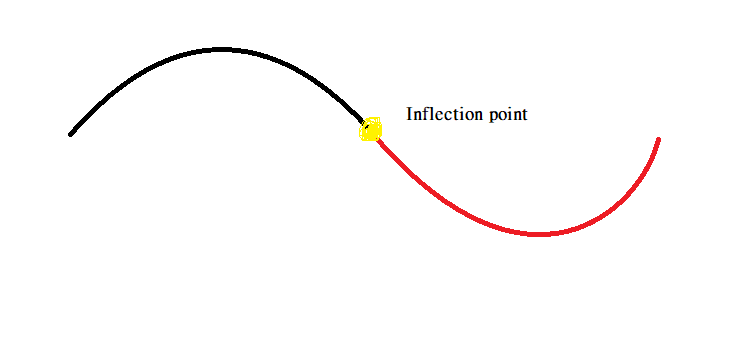
The inflection points are given when the second derivative is equalled to zero. Because the second derivative indicates the change in the concavity of the graph function in the question.

Complete step by step answer:
From the question, we can see that the given equation is
$f(x) = {x^3} - 3{x^2} + 3$
So, we first begin by doing the first derivative of the function and then proceed to the second derivation.
FIRST DERIVATION: -
\[f'(x) = 3{x^2} - 6x\]
Here, we have obtained a simplified form of the equation.
Now, we have to do second derivation of the equation
We get;
\[f''(x) = 6x - 6 = 6(x - 1)\]
The equation obtained is in its simplified form.
For the inflection point, we need to know the point of change of the concavity nature of the function.
The second derivative is negative when $x < 1$, positive when $x > 1$, and zero when $x = 1$ (and of course changes sign as x increases "through" $x = 1$).
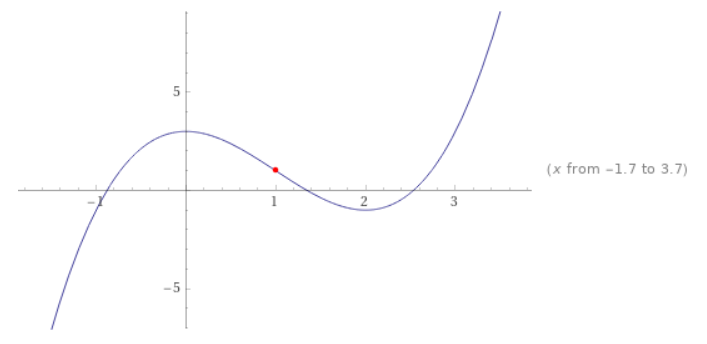
That means the graph of $f(x)$ is concave down when $x < 1$, concave up when $x > 1$, and has an inflection point at $f(x)$. The coordinates of the inflection point are
$(x,y) = (1,f(1)) = (1,1)$
Below is the graphical representation of the given equation with the inflection points marked.

Note: The inflection is the point at which the nature of a concave graph changes from one to another rather than the start points or the endpoint of the curve of the graph of the given function equation.