Question

Find the image of the point P (3, 5, 7) in the plane 2x + y + z = 0.
A.(- 9, -1, 1)
B.(9, 1, 1)
C.(1, 9, 1)
D.(1, -9, 1)

Answer 1

Hint: In these types of questions suppose a point Q \[\left( {{x_1},{\text{ }}{y_1},{\text{ }}{z_1}} \right)\] as image of point P then use the concept of midpoint of a line PQ that says if a line PQ where P \[\left( {{x_1},{\text{ }}{y_1},{\text{ }}{z_1}} \right)\] and point Q \[\left( {{x_2},{\text{ }}{y_2},{\text{ }}{z_2}} \right)\] then if there exist a point M (a, b, c) which divides the Line PQ equally then the coordinates of midpoint can be find as$\dfrac{{{x_1} + {x_2}}}{2} = a$, $\dfrac{{{y_1} + {y_2}}}{2} = b$and \[\dfrac{{{z_1} + {z_2}}}{2} = c\] use this information to approach the solution to the question.

Complete step-by-step answer:
To find the image of point P let assume a point on plane O

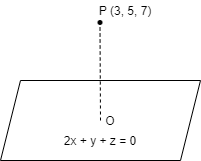
As we know by the given information equation of plane is 2x + y + z = 0 (equation 1)
As we know the equation of plane (ax + by + cz = k) when a line PO where P have some coordinates (p, q, r) and Q with coordinates (x, y, z) is given by \[\dfrac{{p - x}}{a} = \dfrac{{q - y}}{b} = \dfrac{{r - z}}{c} = k\]
Substituting the given values in the above equation
\[\dfrac{{3 - x}}{2} = \dfrac{{5 - y}}{1} = \dfrac{{7 - z}}{1} = k\]
So any point on the line PO can be represented as
x = 3 – 2k, y = 5 – k, z = 7 – k
Therefore the coordinates of point O are [(3 – 2k), (5 – k), (7 – k)]
Substituting these values in the equation 1
2 (3 – 2k) + (5 – k) + (7 – k) = 0
$ \Rightarrow $6 – 4k + 5 – k + 7 – k = 0
$ \Rightarrow $18 – 6k = 0
$ \Rightarrow $k = $\dfrac{{18}}{6}$
$ \Rightarrow $k = 3
Substituting the value of k in coordinates of O
x = 3 – 2(3), y = 5 – 3, z = 7 – 3
$ \Rightarrow $ x = – 3, y = 2, z = 4
Now let’s Q \[\left( {{x_1},{\text{ }}{y_1},{\text{ }}{z_1}} \right)\] be the image of P

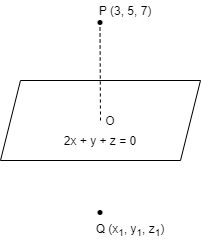
So using the midpoint formula since the distance of point P and point Q are same from point O
Therefore by the midpoint formula
Substituting the values in the midpoint formula$\dfrac{{{x_1} + {x_2}}}{2} = a$, $\dfrac{{{y_1} + {y_2}}}{2} = b$and \[\dfrac{{{z_1} + {z_2}}}{2} = c\]
$\dfrac{{3 + {x_1}}}{2} = - 3$, $\dfrac{{5 + {y_1}}}{2} = 2$and \[\dfrac{{7 + {z_1}}}{2} = 4\]
$ \Rightarrow $${x_1} = - 6 - 3$, ${y_1} = 4 - 5$and \[{z_1} = 8 - 7\]
$ \Rightarrow $${x_1} = - 9$, ${y_1} = - 1$and \[{z_1} = 1\]
Therefore the coordinates of the image of P are (-9, -1, 1)
Hence option A is the correct option.

Note: The term “plane” which was introduced in the above question is the flat surface which exists in 2 dimensions with infinite size this concept can be explained with the help of an example suppose there is a person traveling between the X and Y axis so the surface formed by the X and Y axis is called Plane here the plane formed by X and Y axis is XY plane.