Question

Find the height of the trapezium in which parallel sides are 25 cm and 77 cm and non-parallel sides are 26 cm and 60 cm. Given the area of the trapezium as $1644c{m^2}$.

Answer 1

Hint: First assume the height of the trapezium. After that by symmetry find the portion on the larger side which is the same in length as the smaller side, this divides the trapezium into three areas, that is a triangle then a rectangle, and another triangle. Then add the area of these three and equate it to the total area to get the height of the trapezium.

Complete step-by-step solution:
The pictorial representation of the trapezium ABCD is shown below,

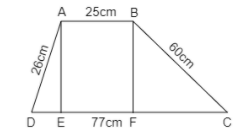
Let AB and CD be the parallel sides and the length of the parallel sides are given which is AB = 25 cm and CD = 77 cm and the length of non-parallel sides are AD = 26 cm and BC = 60 cm.
Let AE and BF are the perpendiculars drawn on side CD respectively. So,
$ \Rightarrow AB = EF = 25cm$
Let the height of the trapezium be h cm. Then,
$ \Rightarrow AE = BF = h{\rm{cm}}$
Let $DE = x$ and $FC = y$.
Let the area of the triangle ADE be ${A_1}$, area of the rectangle ABFE be ${A_2}$ and area of the triangle BFC be ${A_3}$.
Then, from the figure,
$ \Rightarrow DE + EF + FC = 77$
Substitute the values,
$ \Rightarrow x + 25 + y = 77$
Simplify the terms,
$ \Rightarrow x + y = 52$...............….. (1)
Now as we know that the area of the triangle is half multiplied by base time’s perpendicular.
So, the area of the triangle ADE is given by,
$ \Rightarrow {A_1} = \dfrac{1}{2} \times x \times h$
The area of the rectangle ABFE is given by,
$ \Rightarrow {A_2} = 25 \times h$
The area of the triangle BFC is given by,
$ \Rightarrow {A_3} = \dfrac{1}{2} \times y \times h$
So, the area of the trapezium will be the sum of these three areas,
$ \Rightarrow A = {A_1} + {A_2} + {A_3}$
Substitute the values,
$ \Rightarrow 1644 = \dfrac{1}{2}xh + 25h + \dfrac{1}{2}yh$
Take $h$ common on the right side,
$ \Rightarrow 1644 = h\left( {\dfrac{1}{2}x + \dfrac{1}{2}y + 25} \right)$
Now, from equation (1),
$ \Rightarrow 1644 = h\left( {\dfrac{1}{2} \times 26 + 25} \right)$
Cancel out the common factor,
$ \Rightarrow \left( {26 + 25} \right)h = 1644$
Add the terms in the bracket,
$ \Rightarrow 51h = 1644$
Divide both sides by 51,
$\therefore h = 32.24$cm

Hence, the height of the trapezium is 32.24 cm.

Note: A trapezium is a quadrilateral with one pair of sides parallel. It is always advised to form a diagrammatic representation using the information of the question as it helps to understand the geometry of the figure involved. Breaking down the total area into smaller areas of different shapes plays a key role in trapezium area related questions.