Question

Find the height of the parallelogram whose area is $30 cm^2$ and base is 6 cm.

Answer 1

Hint: Use the formula for area of a parallelogram which is given by area = base × height. Upon substitution and further computation, we will get the required answer.

Complete step by step solution: We are given the area of a parallelogram and its base.
We are asked to compute the height of this parallelogram.So, what do we mean by a parallelogram?
It is a type of quadrilateral whose pairs of opposite sides are parallel. Therefore, these opposite sides are of equal length, and the opposite angles of equal measures.
Let’s have a look at the picture of a parallelogram.

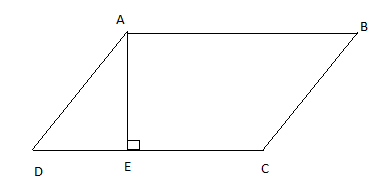
Here, we have drawn a quadrilateral with vertices A, B, C, and D. The foot of the perpendicular from the vertex A to the base DC is labelled as E. We can see that this perpendicular AE is the height of the parallelogram. Thus, in the above figure, ABCD is a parallelogram with base DC and height AE.
Suppose the area of this parallelogram is $30 cm^2$ and base DC is 6 cm.
Then we need to find the height AE.
We will use the formula for the area of a parallelogram.
For any parallelogram, its area = base × height.
Therefore, area of ABCD \[ = DC \times AE\]
\[\begin{array}{*{20}{l}}
{ \Rightarrow 30 = 6 \times AE} \\
{ \Rightarrow AE = 30 \div 6 = 5}
\end{array}\]
Therefore, we have AE = 5 cm.
That is the height of the given parallelogram is 5 cm.

Note: It is not necessary to draw the height of the parallelogram inside it. We may extend the base and drop a perpendicular from any of the vertices above it to get the height as illustrated below:

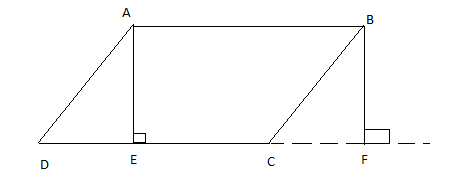
Here BF is also the height of the parallelogram and its length will be the same as the length of AE.