
Find the harmonic conjugate of \[(2,1)\] with respect to \[(4,2)\] and \[(6,3)\]
Answer
568.2k+ views
Hint: Here we have to find the harmonic conjugate of \[(2,1)\] with respect to \[(4,2)\] and\[(6,3)\]. For that, we will name all the points first and then we will assume the ratio in which a point \[(2,1)\] divides the line joining the points \[(4,2)\] and \[(6,3)\] . Then we will apply the section formula to get the ratio. To find the harmonic conjugation the point, we will take the negative of the ratio obtained, which will be the ratio in which the harmonic conjugate of \[(2,1)\] will divide the line segment joining the points \[(4,2)\] and\[(6,3)\]. The obtained point will be the required harmonic conjugation of the given point.
Complete step-by-step answer:
Let’s first name the points:-
\[A(2,1)\], \[B(4,2)\]and \[C(6,3)\]are the given points.
Let the ratio in which the point \[A(2,1)\]divide the line joining the points \[B(4,2)\]and \[C(6,3)\]be \[k:1\]
Let’s draw the line and mark the points.
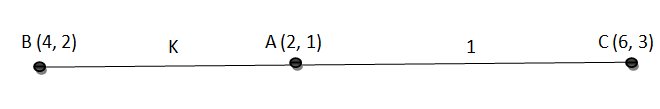
Now, we will apply the section formula.
So the point A from the section formula Now, we will apply the section formula.
So the point A from the section formula \[ = \left( {\dfrac{{k \times 6 + 1 \times 4}}{{k + 1}},\dfrac{{k \times 3 + 1 \times 2}}{{k + 1}}} \right)\]
We will either equate the \[x\] coordinate or y coordinate of point A obtained from the section formula with the coordinates of point A given in the question.
Here we are equating only \[x\] coordinates.
Therefore;
\[ \Rightarrow \dfrac{{k \times 6 + 1 \times 4}}{{k + 1}} = 2\]
Now, by cross multiplication, we get
\[ \Rightarrow k \times 6 + 1 \times 4 = 2\left( {k + 1} \right)\]
On further simplifying the equation, we get
\[ \Rightarrow 6k + 4 = 2k + 2\]
Now, taking all the terms of right hand side of equation to left hand side, we get
\[ \Rightarrow 6k - 2k + 4 - 2 = 0\]
Subtracting the terms, we get
\[ \Rightarrow 4k + 2 = 0\]
On further simplification, we get
\[ \Rightarrow k = - \dfrac{1}{2}\]
Now, to calculate the harmonic conjugate of \[(2,1)\], we will take the negative of the ratio now and apply the same section formula.
The ratio will be \[ - k:1 = 1:2\]
Let the harmonic conjugate of \[(2,1)\] be \[A'(X,Y)\].
So the section formula for point A’ \[=\left( {\dfrac{{6 \times 1 + 2 \times 4}}{{2 + 1}},\dfrac{{3 \times 1 + 2 \times 2}}{{2 + 1}}} \right)\]
On further simplification, we get
Point A’= \[\left( {\dfrac{{14}}{3},\dfrac{7}{3}} \right)\]
So the harmonic conjugate of \[(2,1)\] with respect to \[(4,2)\] and \[(6,3)\] is \[\left( {\dfrac{{14}}{3},\dfrac{7}{3}} \right)\].
Note: Here, we have used the section formula to solve the question. A section formula is a method of finding the coordinates of a point which divide the line in a particular ratio. If that point divides the line in equal parts then the ratio will be equal to \[1:1\].
We can make a mistake by taking only positive ratios and not negative ratios. If we do this we will not get the required harmonic conjugate.
Complete step-by-step answer:
Let’s first name the points:-
\[A(2,1)\], \[B(4,2)\]and \[C(6,3)\]are the given points.
Let the ratio in which the point \[A(2,1)\]divide the line joining the points \[B(4,2)\]and \[C(6,3)\]be \[k:1\]
Let’s draw the line and mark the points.
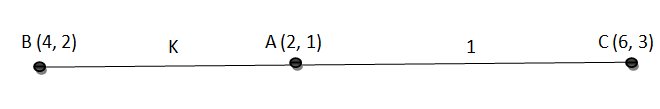
Now, we will apply the section formula.
So the point A from the section formula Now, we will apply the section formula.
So the point A from the section formula \[ = \left( {\dfrac{{k \times 6 + 1 \times 4}}{{k + 1}},\dfrac{{k \times 3 + 1 \times 2}}{{k + 1}}} \right)\]
We will either equate the \[x\] coordinate or y coordinate of point A obtained from the section formula with the coordinates of point A given in the question.
Here we are equating only \[x\] coordinates.
Therefore;
\[ \Rightarrow \dfrac{{k \times 6 + 1 \times 4}}{{k + 1}} = 2\]
Now, by cross multiplication, we get
\[ \Rightarrow k \times 6 + 1 \times 4 = 2\left( {k + 1} \right)\]
On further simplifying the equation, we get
\[ \Rightarrow 6k + 4 = 2k + 2\]
Now, taking all the terms of right hand side of equation to left hand side, we get
\[ \Rightarrow 6k - 2k + 4 - 2 = 0\]
Subtracting the terms, we get
\[ \Rightarrow 4k + 2 = 0\]
On further simplification, we get
\[ \Rightarrow k = - \dfrac{1}{2}\]
Now, to calculate the harmonic conjugate of \[(2,1)\], we will take the negative of the ratio now and apply the same section formula.
The ratio will be \[ - k:1 = 1:2\]
Let the harmonic conjugate of \[(2,1)\] be \[A'(X,Y)\].
So the section formula for point A’ \[=\left( {\dfrac{{6 \times 1 + 2 \times 4}}{{2 + 1}},\dfrac{{3 \times 1 + 2 \times 2}}{{2 + 1}}} \right)\]
On further simplification, we get
Point A’= \[\left( {\dfrac{{14}}{3},\dfrac{7}{3}} \right)\]
So the harmonic conjugate of \[(2,1)\] with respect to \[(4,2)\] and \[(6,3)\] is \[\left( {\dfrac{{14}}{3},\dfrac{7}{3}} \right)\].
Note: Here, we have used the section formula to solve the question. A section formula is a method of finding the coordinates of a point which divide the line in a particular ratio. If that point divides the line in equal parts then the ratio will be equal to \[1:1\].
We can make a mistake by taking only positive ratios and not negative ratios. If we do this we will not get the required harmonic conjugate.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




