Question

Find the force of friction between the box and inclined plane if the mass of the wooden block is 8 Kg which slides down on an inclined plane with the inclination of $30^\circ$ to the horizontal with a constant acceleration of 0.4\[m{s^{ - 2}}\]. [g=10\[m{s^{ - 2}}\] ].
A. 12.2N
B. 24.4N
C. 36.8N
D. 48.8N

Answer 1

Hint: The component of $mg$ along the inclined plane is\[mg\sin \theta \] and the block slides down with the net force $ma$. Now, find the normal acting on the block by the plane. Now, use the formula –
\[a = g\sin \theta - \mu g\cos \theta \]
Where,
\[a\]= Net acceleration of the block
\[\mu \]= Coefficient of friction
\[\theta \]= Angle of inclined plane

Complete step by step answer:
According to the question, it is given that -
Mass of the block $ = m = 8kg$
Net acceleration of the block down the plane\[ = a = 0.4m{s^{ - 2}}\]
Angle of inclination \[ = \theta = {30^ \circ }\]
Value of acceleration due to gravity $ = g = 10$\[m{s^{ - 2}}\]
Let the force of friction = \[f\]
Let the coefficient of friction= \[\mu \]
We have to find the force of friction \[f\]
Let us understand this problem with the help of a diagram

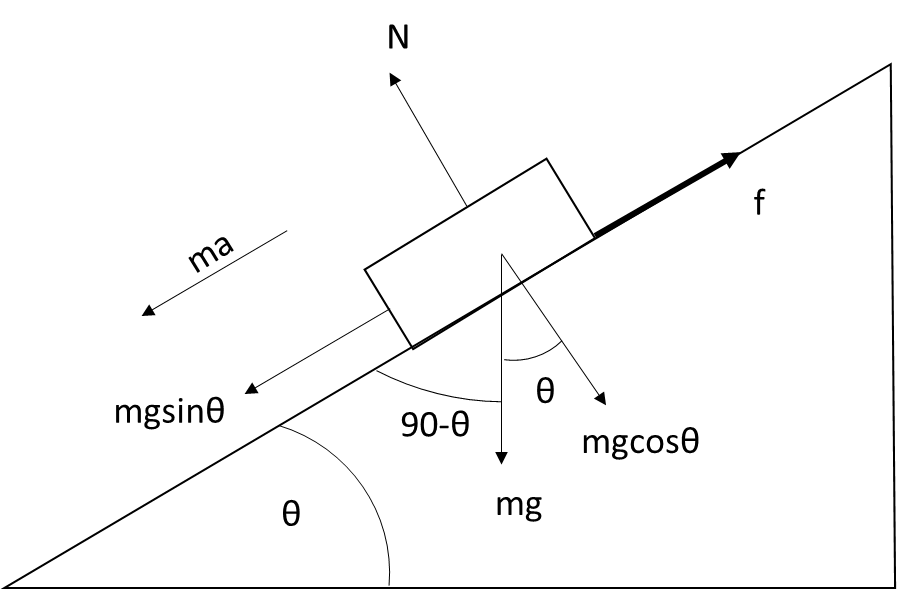
From the above diagram, we can conclude that the inclined plane makes an angle \[\theta \]with the horizontal
As the block acts downwards vertically so, the weight of the block is $mg$.
The component of $mg$ along the inclined plane is \[mg\sin \theta \] & perpendicular to the Inclined plane is \[mg\cos \theta \].
From the definition of frictional force, we know that frictional force $f$ always opposes the relative motion of the block so it will act along the inclined plane upwards
The frictional force is given by \[f = \mu N\]
Where \[N\] is the normal reaction on the block by the plane which acts perpendicular to it and $\mu $ is the coefficient of friction.
Also, from the figure, the block is sliding down with a net force \[ma\]
Where, \[a\] is net acceleration
Writing force equations along the inclined plane & considering downward inclined direction as positive, we get –
\[\Rightarrow mg\sin \theta - f = ma\] ………………...(1)
We know that –
\[f = \mu N\]
Putting value of \[f\] in equation (1) we get
\[\Rightarrow mg\sin \theta - \mu N = ma\] ……………………….(2)
Writing force equations perpendicular to the inclined plane & considering perpendicular upward inclined direction as positive we get.
\[N = mg\cos \theta \]
Putting value of \[N\] in equation (2) we get
\[\Rightarrow mg\sin \theta - \mu mg\cos \theta = ma\]
\[\Rightarrow a = g\sin \theta - \mu g\cos \theta \]
Putting the values of $g$,\[a\], \[\theta \] in above equation
\[\Rightarrow 0.4 = 10\sin {30^0} - \mu 10\cos {30^0}\] (\[\sin {30^0} = \dfrac{1}{2}\],\[\cos {30^0} = \dfrac{{\sqrt 3 }}{2}\])
\[\Rightarrow \mu \dfrac{{10\sqrt 3 }}{2} = \dfrac{{10}}{2} - 0.4\]
Solving the above we get
\[\Rightarrow \mu \]=0.53 (It is a dimensionless quantity)
Now using \[f = \mu N\] & \[N = mg\cos \theta \]
\[\Rightarrow f = \mu mg\cos \theta \]
\[\Rightarrow f = 0.53 \times 8 \times 10 \times \dfrac{{\sqrt 3 }}{2}\]
\[\Rightarrow f = 36.8N\]

$\therefore$ The force of friction between the box and inclined plane 36.8N. Hence, option (C) is correct.

Note:
This problem could also have been solved directly from equation (1)
\[mg\sin \theta - f = ma\]
\[\Rightarrow f = ma - mg\sin \theta \]
\[\Rightarrow f = 8 \times 0.4 - 8 \times 10\sin {30^0}\]
\[\Rightarrow f = 8 \times 0.4 - 8 \times 10 \times \dfrac{1}{2}\]
\[\Rightarrow f = - 36.8N\]
Here, the negative sign shows friction acts opposite to the direction of motion.