Question

How do you find the foci and sketch the ellipse $9{x^2} + 4{y^2} = 16$?

Answer 1

Hint: We first have to transform the given equation into the standard form of equation of the ellipse given as $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$. To find the foci, we have to find $a$ and $b$, the larger one will be the major-axis and the smaller one will be the minor-axis of the given ellipse. Using this we can find the foci of the ellipse at $\sqrt {{a^2} - {b^2}} $ on the major-axis on both sides from the origin. We will then use all this information to sketch the ellipse.

Complete step by step solution:
We are given the equation of the ellipse $9{x^2} + 4{y^2} = 16$
To transform it into standard form, we can write it as,
$
  9{x^2} + 4{y^2} = 16 \\
   \Rightarrow \dfrac{{9{x^2}}}{{16}} + \dfrac{{4{y^2}}}{{16}} = 1 \\
   \Rightarrow \dfrac{{{x^2}}}{{\left( {\dfrac{{16}}{9}} \right)}} + \dfrac{{{y^2}}}{{\left( {\dfrac{{16}}{4}} \right)}} = 1 \\
   \Rightarrow \dfrac{{{x^2}}}{{\left( {\dfrac{{16}}{9}} \right)}} + \dfrac{{{y^2}}}{4} = 1 \\
   \Rightarrow \dfrac{{{x^2}}}{{{{\left( {\dfrac{4}{3}} \right)}^2}}} + \dfrac{{{y^2}}}{{{2^2}}} = 1 \\
$
So we get $a = \dfrac{4}{3}$ and $b = 2$
Therefore, major-axis is $2$ (on the y-axis) and minor-axis is $\dfrac{4}{3}$ (on the x-axis).
The foci of the ellipse is given at \[c = \sqrt {{b^2} - {a^2}} \].
\[
  c = \sqrt {{b^2} - {a^2}} \\
   \Rightarrow c = \sqrt {{2^2} - {{\left( {\dfrac{4}{3}} \right)}^2}} \\
   \Rightarrow c = \sqrt {4 - \left( {\dfrac{{16}}{9}} \right)} \\
   \Rightarrow c = \sqrt {\left( {\dfrac{{36 - 16}}{9}} \right)} \\
   \Rightarrow c = \sqrt {\left( {\dfrac{{20}}{9}} \right)} = \dfrac{{2\sqrt 5 }}{3} \\
\]
Thus, the foci is at $\left( {0,{\kern 1pt} {\kern 1pt} {\kern 1pt} \dfrac{{2\sqrt 5 }}{3}} \right)$ and $\left( {0,{\kern 1pt} {\kern 1pt} {\kern 1pt} - \dfrac{{2\sqrt 5 }}{3}} \right)$
Now to sketch the ellipse we plot four points of the ellipse, two vertices on the major axis and two vertices on the minor axis.
The vertices on major axis are $(0,{\kern 1pt} {\kern 1pt} {\kern 1pt} b)$ and $(0,{\kern 1pt} {\kern 1pt} {\kern 1pt} - b)$, i.e. $(0,{\kern 1pt} {\kern 1pt} {\kern 1pt} 2)$ and $(0,{\kern 1pt} {\kern 1pt} {\kern 1pt} - 2)$
The vertices on minor axis are $(a,{\kern 1pt} {\kern 1pt} {\kern 1pt} 0)$ and $( - a,{\kern 1pt} {\kern 1pt} {\kern 1pt} 0)$, i.e. $(\dfrac{4}{3},{\kern 1pt} {\kern 1pt} {\kern 1pt} 0)$ and $( - \dfrac{4}{3},{\kern 1pt} {\kern 1pt} {\kern 1pt} 0)$
Then we join these four points as a curve of an ellipse.
The graph of the given equation is shown below,

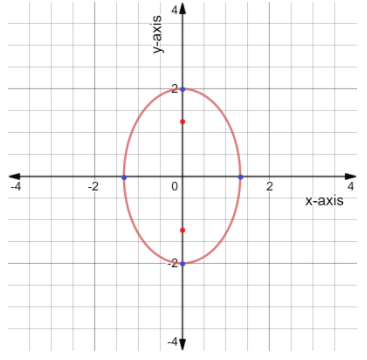
Note: The foci of the ellipse are at $e$ times the semi-major axis, where $e$ is the eccentricity of the ellipse. We have to be careful about the major-axis and minor-axis while calculating the foci and sketching the ellipse. The foci are always situated between the origin and the vertices on the major-axis.