
How do you find the exact values of ${{\sin }^{-1}}\left( \dfrac{\sqrt{2}}{2} \right)$?
Answer
556.8k+ views
Hint: In this problem, we have to find the value of the angle given. We will be using trigonometric ratios and some properties of inverse functions. Trigonometric functions will be applied on the right angled triangle with given sides and angles. Mainly we have to solve the whole question using Pythagoras theorem:
${{\left( hypotenuse \right)}^{2}}={{\left( base \right)}^{2}}+{{\left( perpendicular \right)}^{2}}$
Now, solve the problem and find its solution.
Complete step-by-step answer:
Here, the basic function of the trigonometry is used i.e. sine. Even some functions can be derived using this function. They are:
$\Rightarrow $cosec$\theta $ = $\dfrac{1}{\sin \theta }$
$\Rightarrow $sec$\theta $ = $\dfrac{1}{\cos \theta }$
$\Rightarrow $tan$\theta $ = $\dfrac{\sin \theta }{\cos \theta }$ = $\dfrac{1}{\cot \theta }$
$\Rightarrow $cot$\theta $ = $\dfrac{1}{\tan \theta }$ = $\dfrac{\cos \theta }{\sin \theta }$
Let’s see how we actually find the angle of a triangle using sine function.
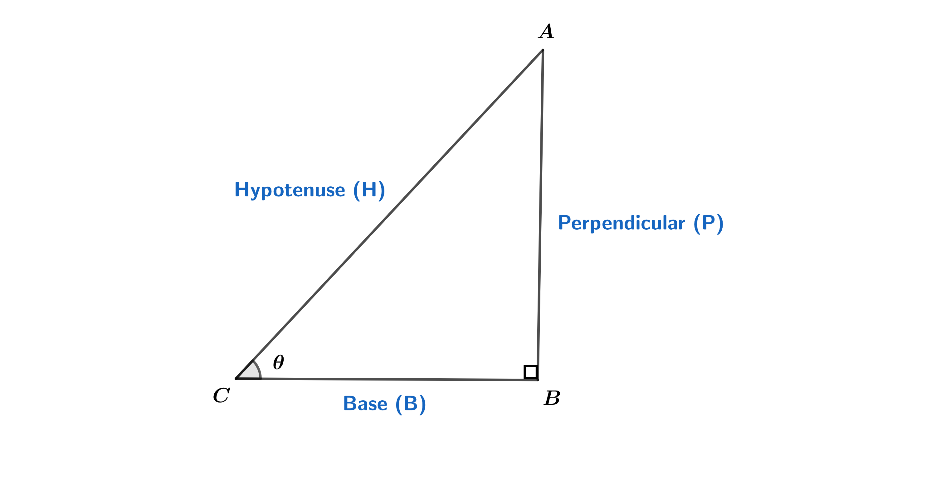
So, from figure, sin$\theta $ = $\dfrac{perpendicular(P)}{hypotenuse(H)}$
Let’s assume a triangle which is right angled at B. It’s sides are $\dfrac{\sqrt{2}}{2},\dfrac{\sqrt{2}}{2}$ and 1. Angles are: $\angle A=\dfrac{\pi }{4},\angle B=\dfrac{\pi }{2},\angle C=\dfrac{\pi }{4}$
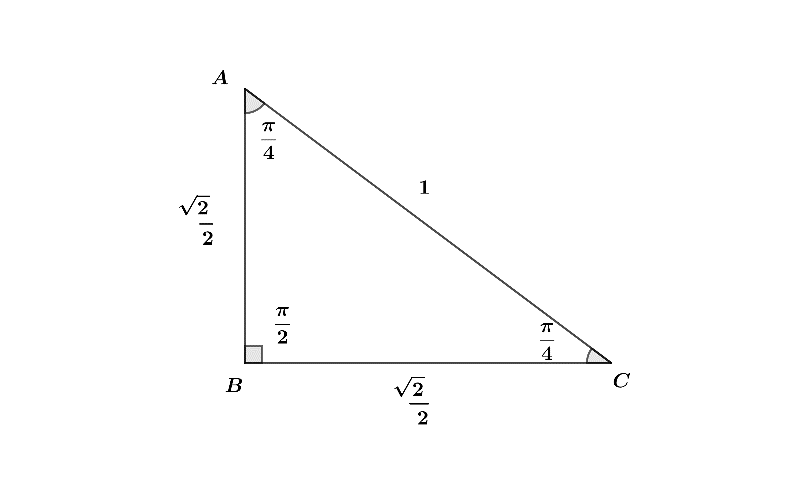
Let’s check whether the triangle satisfies Pythagoras theorem or not. According to Pythagoras theorem:
${{\left( hypotenuse \right)}^{2}}={{\left( base \right)}^{2}}+{{\left( perpendicular \right)}^{2}}$
$\Rightarrow {{\left( AC \right)}^{2}}={{\left( BC \right)}^{2}}+{{\left( AB \right)}^{2}}$
Now, put the values for base and perpendicular:
$\Rightarrow {{\left( AC \right)}^{2}}={{\left( \dfrac{\sqrt{2}}{2} \right)}^{2}}+{{\left( \dfrac{\sqrt{2}}{2} \right)}^{2}}$
Open the brackets and solve:
$\Rightarrow {{\left( AC \right)}^{2}}=\dfrac{2}{4}+\dfrac{2}{4}$
On adding, we get:
$\Rightarrow {{\left( AC \right)}^{2}}=\dfrac{4}{4}$
Cancel the like terms:
$\Rightarrow AC=\sqrt{1}$
$\therefore $AC = 1
Which proves that it satisfies Pythagoras theorem.
As we know that, sin$\theta $ = $\dfrac{perpendicular(P)}{hypotenuse(H)}$
According to the triangle,
$\Rightarrow \sin \left( \dfrac{\pi }{4} \right)=\dfrac{\sqrt{2}}{2}$
When we take to the other side, it will form an inverse function. So,
$\Rightarrow \dfrac{\pi }{4}={{\sin }^{-1}}\left( \dfrac{\sqrt{2}}{2} \right)$
So we get the value as $\dfrac{\pi }{4}$.
Note: Here, Pythagora's theorem is just used to check whether we have taken right sides and angles for right angled triangle or not. As we know that trigonometric functions work only on right angled triangles. Knowledge of basic trigonometric functions is very much necessary for solving such questions.
${{\left( hypotenuse \right)}^{2}}={{\left( base \right)}^{2}}+{{\left( perpendicular \right)}^{2}}$
Now, solve the problem and find its solution.
Complete step-by-step answer:
Here, the basic function of the trigonometry is used i.e. sine. Even some functions can be derived using this function. They are:
$\Rightarrow $cosec$\theta $ = $\dfrac{1}{\sin \theta }$
$\Rightarrow $sec$\theta $ = $\dfrac{1}{\cos \theta }$
$\Rightarrow $tan$\theta $ = $\dfrac{\sin \theta }{\cos \theta }$ = $\dfrac{1}{\cot \theta }$
$\Rightarrow $cot$\theta $ = $\dfrac{1}{\tan \theta }$ = $\dfrac{\cos \theta }{\sin \theta }$
Let’s see how we actually find the angle of a triangle using sine function.

So, from figure, sin$\theta $ = $\dfrac{perpendicular(P)}{hypotenuse(H)}$
Let’s assume a triangle which is right angled at B. It’s sides are $\dfrac{\sqrt{2}}{2},\dfrac{\sqrt{2}}{2}$ and 1. Angles are: $\angle A=\dfrac{\pi }{4},\angle B=\dfrac{\pi }{2},\angle C=\dfrac{\pi }{4}$
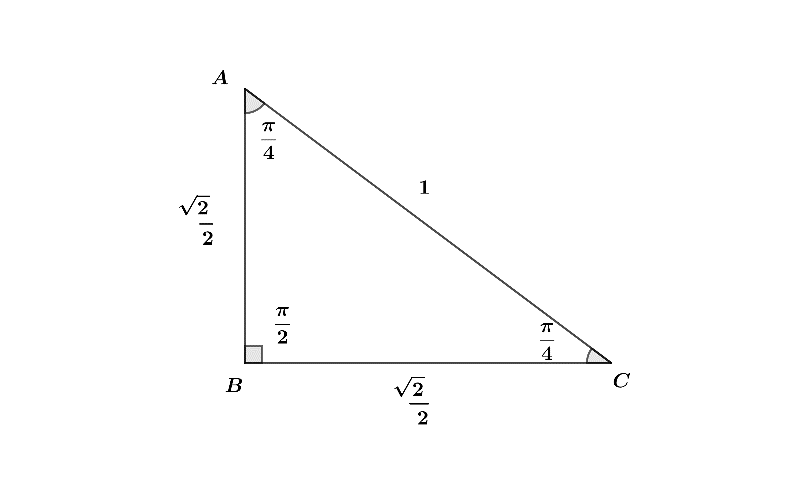
Let’s check whether the triangle satisfies Pythagoras theorem or not. According to Pythagoras theorem:
${{\left( hypotenuse \right)}^{2}}={{\left( base \right)}^{2}}+{{\left( perpendicular \right)}^{2}}$
$\Rightarrow {{\left( AC \right)}^{2}}={{\left( BC \right)}^{2}}+{{\left( AB \right)}^{2}}$
Now, put the values for base and perpendicular:
$\Rightarrow {{\left( AC \right)}^{2}}={{\left( \dfrac{\sqrt{2}}{2} \right)}^{2}}+{{\left( \dfrac{\sqrt{2}}{2} \right)}^{2}}$
Open the brackets and solve:
$\Rightarrow {{\left( AC \right)}^{2}}=\dfrac{2}{4}+\dfrac{2}{4}$
On adding, we get:
$\Rightarrow {{\left( AC \right)}^{2}}=\dfrac{4}{4}$
Cancel the like terms:
$\Rightarrow AC=\sqrt{1}$
$\therefore $AC = 1
Which proves that it satisfies Pythagoras theorem.
As we know that, sin$\theta $ = $\dfrac{perpendicular(P)}{hypotenuse(H)}$
According to the triangle,
$\Rightarrow \sin \left( \dfrac{\pi }{4} \right)=\dfrac{\sqrt{2}}{2}$
When we take to the other side, it will form an inverse function. So,
$\Rightarrow \dfrac{\pi }{4}={{\sin }^{-1}}\left( \dfrac{\sqrt{2}}{2} \right)$
So we get the value as $\dfrac{\pi }{4}$.
Note: Here, Pythagora's theorem is just used to check whether we have taken right sides and angles for right angled triangle or not. As we know that trigonometric functions work only on right angled triangles. Knowledge of basic trigonometric functions is very much necessary for solving such questions.
Recently Updated Pages
Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Physics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




