
How do you find the exact value of \[\tan x - 3\cot x = 0\] in the interval \[0 \leqslant x < {360^ \circ }\]
Answer
543.9k+ views
Hint: We use the substitution of cotangent in terms of tangent of the function. Equate the value to zero and write the value of tangent of angle. Use a quadrant diagram to write the values between 0 and \[{360^ \circ }\].
\[\cot x = \dfrac{1}{{\tan x}}\]
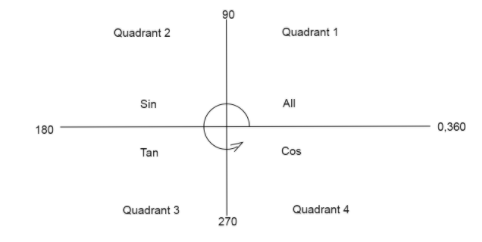
We know the values of all trigonometric angles are positive in the first quadrant.
Values of only \[\sin \theta \] are positive in the second quadrant.
Values of only \[\tan \theta \] are positive in the third quadrant.
Values of only \[\cos \theta \] are positive in the fourth quadrant.
Complete step-by-step solution:
We have to solve for the value of x in \[\tan x - 3\cot x = 0\] … (1)
Substitute the value of \[\cot x = \dfrac{1}{{\tan x}}\]in equation (1)
\[ \Rightarrow \tan x - \dfrac{3}{{\tan x}} = 0\]
Take LCM in left hand side of the equation
\[ \Rightarrow \dfrac{{{{\tan }^2}x - 3}}{{\tan x}} = 0\]
Cross multiply the denominator of left hand side of the equation to right hand side of the equation
\[ \Rightarrow {\tan ^2}x - 3 = 0\]
Shift constant value to right hand side of the equation
\[ \Rightarrow {\tan ^2}x = 3\]
Take square root on both sides of the equation
\[ \Rightarrow \sqrt {{{\tan }^2}x} = \pm \sqrt 3 \]
Cancel square root by square power on left side of the equation
\[ \Rightarrow \tan x = \pm \sqrt 3 \] … (1)
Then we can write \[\tan x = \sqrt 3 \] and \[\tan x = - \sqrt 3 \]
We know that the value of \[\tan \dfrac{\pi }{3} = \sqrt 3 \]
Also, we know tan is an odd function, so, \[\tan ( - x) = - \tan x\]and that tangent function is positive in the first and third quadrant and is negative in the second and fourth quadrant.
Then we can write \[\tan x = \sqrt 3 \] gives the angles \[\dfrac{\pi }{3}\]and \[\pi + \dfrac{\pi }{3} = \dfrac{{4\pi }}{3}\]
So, the angles for \[\tan x = \sqrt 3 \] are \[{60^ \circ }\]and \[{240^ \circ }\] between \[0 \leqslant x < {360^ \circ }\]
And \[\tan x = - \sqrt 3 \] gives the angles \[\pi - \dfrac{\pi }{3} = \dfrac{{2\pi }}{3}\]and \[2\pi - \dfrac{\pi }{3} = \dfrac{{5\pi }}{3}\]
So, the angles for \[\tan x = - \sqrt 3 \] are \[{120^ \circ }\] and \[{300^ \circ }\] between \[0 \leqslant x < {360^ \circ }\]
\[\therefore \]The exact value of \[\tan x - 3\cot x = 0\] in the interval \[0 \leqslant x < {360^ \circ }\] is \[{60^ \circ },{120^ \circ },{240^ \circ },{300^ \circ }\]
Note: Many students make the mistake of writing the square root of 3 as only positive value which is wrong as we know the square root gives both negative and positive value of the number. Keep in mind we can use table for trigonometric terms if we don’t remember the values at some common angles \[{0^ \circ },{30^ \circ },{45^ \circ },{60^ \circ },{90^ \circ }\]
\[\cot x = \dfrac{1}{{\tan x}}\]
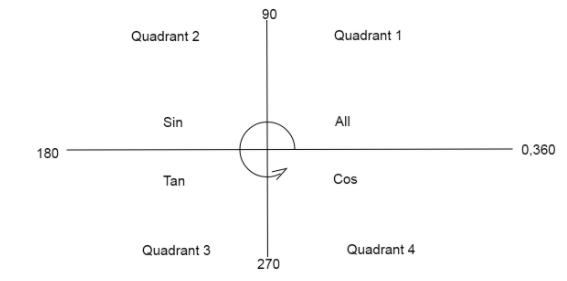
We know the values of all trigonometric angles are positive in the first quadrant.
Values of only \[\sin \theta \] are positive in the second quadrant.
Values of only \[\tan \theta \] are positive in the third quadrant.
Values of only \[\cos \theta \] are positive in the fourth quadrant.

Complete step-by-step solution:
We have to solve for the value of x in \[\tan x - 3\cot x = 0\] … (1)
Substitute the value of \[\cot x = \dfrac{1}{{\tan x}}\]in equation (1)
\[ \Rightarrow \tan x - \dfrac{3}{{\tan x}} = 0\]
Take LCM in left hand side of the equation
\[ \Rightarrow \dfrac{{{{\tan }^2}x - 3}}{{\tan x}} = 0\]
Cross multiply the denominator of left hand side of the equation to right hand side of the equation
\[ \Rightarrow {\tan ^2}x - 3 = 0\]
Shift constant value to right hand side of the equation
\[ \Rightarrow {\tan ^2}x = 3\]
Take square root on both sides of the equation
\[ \Rightarrow \sqrt {{{\tan }^2}x} = \pm \sqrt 3 \]
Cancel square root by square power on left side of the equation
\[ \Rightarrow \tan x = \pm \sqrt 3 \] … (1)
Then we can write \[\tan x = \sqrt 3 \] and \[\tan x = - \sqrt 3 \]
We know that the value of \[\tan \dfrac{\pi }{3} = \sqrt 3 \]
Also, we know tan is an odd function, so, \[\tan ( - x) = - \tan x\]and that tangent function is positive in the first and third quadrant and is negative in the second and fourth quadrant.

Then we can write \[\tan x = \sqrt 3 \] gives the angles \[\dfrac{\pi }{3}\]and \[\pi + \dfrac{\pi }{3} = \dfrac{{4\pi }}{3}\]
So, the angles for \[\tan x = \sqrt 3 \] are \[{60^ \circ }\]and \[{240^ \circ }\] between \[0 \leqslant x < {360^ \circ }\]
And \[\tan x = - \sqrt 3 \] gives the angles \[\pi - \dfrac{\pi }{3} = \dfrac{{2\pi }}{3}\]and \[2\pi - \dfrac{\pi }{3} = \dfrac{{5\pi }}{3}\]
So, the angles for \[\tan x = - \sqrt 3 \] are \[{120^ \circ }\] and \[{300^ \circ }\] between \[0 \leqslant x < {360^ \circ }\]
\[\therefore \]The exact value of \[\tan x - 3\cot x = 0\] in the interval \[0 \leqslant x < {360^ \circ }\] is \[{60^ \circ },{120^ \circ },{240^ \circ },{300^ \circ }\]
Note: Many students make the mistake of writing the square root of 3 as only positive value which is wrong as we know the square root gives both negative and positive value of the number. Keep in mind we can use table for trigonometric terms if we don’t remember the values at some common angles \[{0^ \circ },{30^ \circ },{45^ \circ },{60^ \circ },{90^ \circ }\]
| ANGLEFUNCTION | \[{0^ \circ }\] | \[{30^ \circ }\] | \[{45^ \circ }\] | \[{60^ \circ }\] | \[{90^ \circ }\] |
| Sin | 0 | \[\dfrac{1}{2}\] | \[\dfrac{1}{{\sqrt 2 }}\] | \[\dfrac{{\sqrt 3 }}{2}\] | 1 |
| Cos | 1 | \[\dfrac{{\sqrt 3 }}{2}\] | \[\dfrac{1}{{\sqrt 2 }}\] | \[\dfrac{1}{2}\] | 0 |
| Tan | 0 | \[\dfrac{1}{{\sqrt 3 }}\] | 1 | \[\sqrt 3 \] | Not defined |
Recently Updated Pages
Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
What are the major means of transport Explain each class 12 social science CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Draw a ray diagram of compound microscope when the class 12 physics CBSE

How is democracy better than other forms of government class 12 social science CBSE

What is virtual and erect image ?

Explain the energy losses in the transformer How are class 12 physics CBSE




