Question

How do you find the exact value of $\tan \dfrac{\pi }{4}$?

Answer 1

Hint: Start with assuming an isosceles right-angled triangle $\Delta MNP$ and with right angle at N and sides MN and NP equal to each other. This gives us $\angle NMP = \angle NPM = 45^\circ $ . Now use the definition of the tangent function, find the expression for it. Now substitute the values in it and simplify it to get the required value of $\tan \dfrac{\pi }{4}$ .

Complete step-by-step answer:
Here in this question, we are given an expression in tangent function, i.e. $\tan \dfrac{\pi }{4}$ and we have to find the exact value for this expression.
Before starting with the solution, we must understand a few concepts about tangent functions. Tan function (or tangent function) in a triangle is the ratio of the opposite side to that of the adjacent side. The tangent function is one of the three main primary trigonometric functions. In a right-triangle, tan is defined as the ratio of the length of the perpendicular side to that of the adjacent side i.e. the base.
As we know that an angle of $\pi $ radians is equal to $180^\circ $ angle.
$ \Rightarrow \tan \dfrac{\pi }{4} = \tan \left( {\dfrac{{180^\circ }}{4}} \right) = \tan 45^\circ $
For finding this value, we first take an isosceles right-angle triangle $\Delta MNP$ with sides of length ‘m’ units. In this triangle, we have two equal sides, i.e. $MN = NP = m{\text{ units}}$ . Since the two adjacent sides are equal in a triangle, therefore the angles opposite to these sides are also equal. Thus we have:
$ \Rightarrow MN = NP = m$ and $\angle PMN = \angle MPN = \dfrac{{\angle MNP}}{2} = \dfrac{{90^\circ }}{2} = 45^\circ $
This information can be represented in a diagram as:

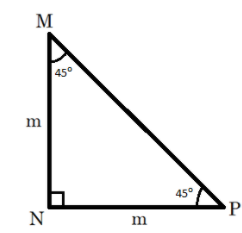
We can use the Pythagoras theorem, which states that the square of the length of the hypotenuse of a right triangle equals the sum of the squares of the lengths of the other two sides. By this theorem, in the triangle $\Delta MNP$ , we get:
$ \Rightarrow P{M^2} = M{N^2} + N{P^2}$
Now let’s substitute the known values in this equation:
$ \Rightarrow P{M^2} = M{N^2} + N{P^2} \Rightarrow P{M^2} = {m^2} + {m^2}$
This equation can be easily solved to find the unknown length of hypotenuse PM
$ \Rightarrow P{M^2} = {m^2} + {m^2} \Rightarrow P{M^2} = 2{m^2}$
Taking square root on both the sides, we have:
$ \Rightarrow \sqrt {P{M^2}} = \sqrt {2{m^2}} \Rightarrow PM = \sqrt 2 m$
Therefore, we get the length of the hypotenuse PM as $\sqrt 2 m$
Now, according to the definition of the tangent function, we have the relation:
$ \Rightarrow \tan \theta = \dfrac{{Perpendicular}}{{Base}}$
For the triangle $\Delta MNP$, using the tangent function in angle $\angle PMN$, we can write it as:
$ \Rightarrow \tan 45^\circ = \dfrac{{Perpendicular}}{{Base}} = \dfrac{{NP}}{{MN}} = \dfrac{m}{m}$
This can be simplified by dividing numerator and denominator by ‘m’
\[ \Rightarrow \tan 45^\circ = \dfrac{m}{m} = 1\]
Therefore, we get the required value of $\tan \dfrac{\pi }{4}$ or $\tan 45^\circ $ as $1$.

Note: In this question, we used an example of an equilateral triangle that was a crucial part of the solution. Notice that the value of $\tan 45^\circ $ does not depend on the sides of the triangle. An alternative approach to this problem can be to find the value of $\sin 45^\circ {\text{ & }}\cos 45^\circ $ and then use the relation $\tan \theta = \dfrac{{\sin \theta }}{{\cos \theta }}$ .