Question

How do you find the exact area of a triangle with a base of square root 30 meters and a height of square root 6 meters ?

Answer 1

Hint: Here in this question, we have to find the exact value of area of triangle using the formula of area of triangle i.e., \[Area = \dfrac{1}{2} \times base \times height\] then substitute the given value of base and height on simplification using the basic multiplication operation we get the required area of the triangle.

Complete step by step solution:
The area of a triangle is defined as the total region that is enclosed by the three sides of any particular triangle. Basically, it is equal to half of the base times height, i.e. \[Area = \dfrac{1}{2} \times base \times height\] or \[A = \dfrac{1}{2} \times b \times h\]. Hence, to find the area of a tri-sided polygon, we have to know the base (b) and height (h) of it.

Consider triangle \[\Delta \,ABC\] where BC is the base of triangle its length is \[\sqrt {30} \] meter i.e., \[BC = \sqrt {30} \,m\]. And draw the line AD which is perpendicular to the line BC i.e., \[AD \bot BC\]. AD is the height of the given triangle, its length is \[\sqrt 6 \] meter i.e., \[AD = \sqrt 6 \,m\].

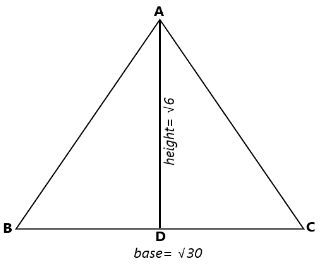
The formula of area of triangle is
\[Area = \dfrac{1}{2} \times base \times height\]
The area of triangle \[\Delta \,ABC\] is
\[Area = \dfrac{1}{2} \times BC \times AD\]
\[ \Rightarrow \,\,Area = \dfrac{1}{2} \times \sqrt {30} \times \sqrt 6 \]
Using the property of multiplication of radicals i.e., \[\sqrt {ab} = \sqrt a \cdot \sqrt b \]
\[ Area = \dfrac{1}{2} \times \sqrt {30 \times 6} \]
\[ \Rightarrow \,\,Area = \dfrac{1}{2} \times \sqrt {180} \]
180 can be written as \[36 \times 5\], then
\[ Area = \dfrac{1}{2} \times \sqrt {36 \times 5} \]
Using the property of radicals
\[ \Rightarrow \,\,Area = \dfrac{1}{2} \times \sqrt {36} \times \sqrt 5 \]
As we know, 36 is the square number of 6
\[ Area = \dfrac{1}{2} \times \sqrt {{6^2}} \times \sqrt 5 \]
\[ \Rightarrow \,\,Area = \dfrac{1}{2} \times 6\sqrt 5 \]
On simplification, we get
\[ \therefore \,\,Area = 3\sqrt 5 \] meter.

Hence, the area of the triangle is \[3\sqrt 5 \] meter.

Note: While determining the area we use the formula. The formula is \[A = \dfrac{1}{2} \times b \times h\]. The unit for the perimeter will be the same as the unit of the length of a side or triangle. Whereas the unit for the area will be the square of the unit of the length of a triangle. We should not forget to write the unit.