Question

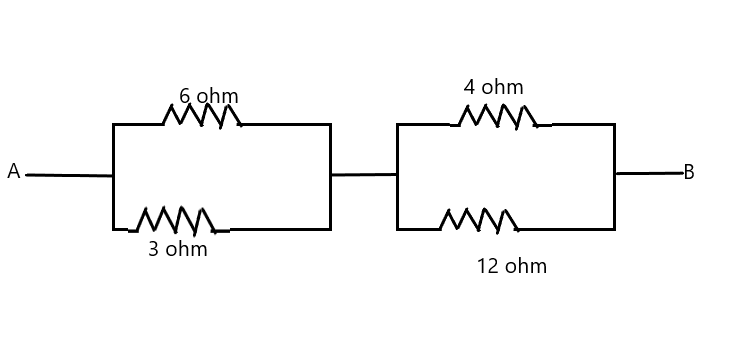
Find the equivalent resistance between A and B.

Answer 1

Hint: In this question, we use the concept of equivalent resistance that is when we connect two resistance in series for example let \[{R_1}\] and \[{R_2}\] be connected in series then equivalent resistance \[{R_{eq}} = {R_1} + {R_2}\] and when we connect these resistances in parallel we get equivalent resistances as $\dfrac{1}{{R{}_{eq}}} = \dfrac{1}{{R{}_1}} + \dfrac{1}{{R{}_2}}$ . Using this we can solve the question that is \[\dfrac{1}{{R{}_{6,3}}} = \dfrac{1}{6} + \dfrac{1}{3}\] and \[\dfrac{1}{{R{}_{4,12}}} = \dfrac{1}{4} + \dfrac{1}{{12}}\] as they are in parallel.

Step-By-Step answer:
We know when we connect two resistance in series, for example, let \[{R_1}\] and \[{R_2}\] be connected in series then the total or equivalent resistance will increase and it becomes
\[{R_{eq}} = {R_1} + {R_2}\] ---------------------------- (1)
Similarly when we connect two resistance that is \[{R_1}\] and \[{R_2}\] in parallel then the total or equivalent resistance will decrease and it becomes
$\dfrac{1}{{R{}_{eq}}} = \dfrac{1}{{R{}_1}} + \dfrac{1}{{R{}_2}}$ -------------------------- (2)
In this question we first consider 6 ohm and 3 ohm resistances, we can see they are connected in parallel so using equation (1) we get the equivalent resistance $R{}_{6,3}$ as
\[\dfrac{1}{{R{}_{6,3}}} = \dfrac{1}{6} + \dfrac{1}{3}\]
\[ \Rightarrow \dfrac{1}{{R{}_{6,3}}} = \dfrac{{3 + 6}}{{6 \times 3}} = \dfrac{9}{{18}} = \dfrac{1}{3}\]
\[ \Rightarrow R{}_{6,3} = 3\] ohm
Now consider 4 ohm and 12 ohm resistances, we can see they are connected in parallel so again using equation (1) we get the equivalent resistance $R{}_{4,12}$ as
\[\dfrac{1}{{R{}_{4,12}}} = \dfrac{1}{4} + \dfrac{1}{{12}}\]
\[ \Rightarrow \dfrac{1}{{R{}_{4,12}}} = \dfrac{{12 + 4}}{{4 \times 12}} = \dfrac{{16}}{{48}} = \dfrac{1}{3}\]
\[ \Rightarrow R{}_{4,12} = 3\] ohm
Now our figure is reduced as shown in figure 1,

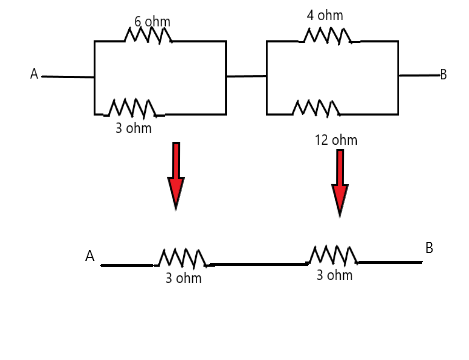
Now we take these two 3 ohm resistance in series and find the equivalent resistance as
\[ \Rightarrow R{}_{3,3} = 3 + 3 = 6\]
\[ \Rightarrow R{}_{3,3} = 6\] ohm
Hence the equivalent resistance of the given network becomes 6 ohm as shown in figure 2,

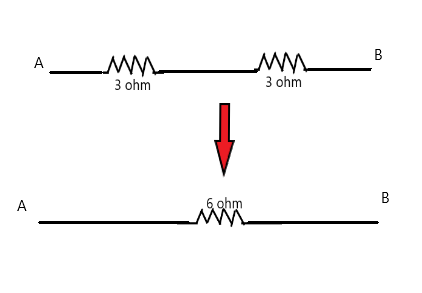
Figure 2

Note: For these types of questions we need to know some basic concepts of electric circuits such as how to find equivalent resistances when connected in parallel or series, how to apply current divider rule in a parallel circuit, and how to apply voltage divider in a series circuit.