Question

Find the equation of the tangents to the circle $ {{x}^{2}}+{{y}^{2}}=4 $ which are perpendicular to the line $ 12x-5y+9=0 $ . Also find the points of contact.

Answer 1

Hint: We first need to write the equation of the line given in $ y=mx+c $ the form. Then we know that the product of slopes of two perpendicular lines is -1. Therefore, $ {{m}_{1}}.{{m}_{2}}=-1 $ .To find the value of the c, we can use the formula for perpendicular distance (d) of a line $ Ax+By+C=0 $ from a point $ O\left( {{x}_{1}},{{y}_{1}} \right) $ is given by, $ d=\dfrac{\left| A{{x}_{1}}+B{{y}_{1}}+C \right|}{\sqrt{{{A}^{2}}+{{B}^{2}}}} $ .

Complete step-by-step answer:
Let’s analyze the circle first. We have given the equation of the circle as $ {{x}^{2}}+{{y}^{2}}=4 $
Comparing with the equation, $ {{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}} $ , where (a,b) is the centre of the circle and r is the radius of the circle.
Therefore, we get, the center of the circle is (a, b) = (0,0) and $ {{r}^{2}}=4 $ ,
Taking the square root, we get,
 $ r=2 $ .
Now, let’s consider the line we have been given.
The equation of the line that is given is $ 12x-5y+9=0 $ .
Writing the equation in the form $ y=mx+c $ we get,
 $ \begin{align}
  & 12x-5y+9=0 \\
 & 5y=12x+9 \\
 & y=\dfrac{12}{5}x+\dfrac{9}{5}..........(i) \\
\end{align} $
Comparing with $ y=mx+c $ we get, $ {{m}_{1}}=\dfrac{12}{5} $ and $ c=\dfrac{9}{5} $ .
We need to find the tangent that is perpendicular to this line.
We need to know that the product of slopes of two perpendicular lines is -1.
Therefore, we know the value of $ {{m}_{1}}=\dfrac{12}{5} $ we need to find the slope of $ {{m}_{2}} $ .
 $ {{m}_{1}}.{{m}_{2}}=-1...............(ii) $
Therefore, by substituting we get,
 $ \dfrac{12}{5}\times {{m}_{2}}=-1 $
Solving we get,
 $ \begin{align}
  & {{m}_{2}}=-1\times \dfrac{5}{12} \\
 & =\dfrac{-5}{12}
\end{align} $
Therefore, the slope of the tangent is $ \dfrac{-5}{12} $ .
Hence, by $ y=mx+c $ substituting the value of $ {{m}_{2}} $ we get,
 $ y=\dfrac{-5}{12}x+c.......................(iii) $
Now, we need to find the value of c.
This is the equation of the tangent therefore, it intersects the circle at that point and the centre is at the distance of radius.
We can use the formula for perpendicular distance (d) of a line $ Ax+By+C=0 $ from a point $ O\left( {{x}_{1}},{{y}_{1}} \right) $ is given by,
 $ d=\dfrac{\left| A{{x}_{1}}+B{{y}_{1}}+C \right|}{\sqrt{{{A}^{2}}+{{B}^{2}}}}..........(iv) $
Here, d = radius = 2units, A = $ \dfrac{-5}{12} $ , B = -1, C = c, $ \left( {{x}_{1}},{{y}_{1}} \right)=\left( 0,0 \right) $ .
Substituting we get,
 $ 2=\dfrac{\left| \left( \dfrac{-5}{12}\times 0 \right)+\left( -1\times 0 \right)+c \right|}{\sqrt{{{\left( \dfrac{-5}{12} \right)}^{2}}+{{\left( -1 \right)}^{2}}}} $
Solving the equation, we get,
 $ \begin{align}
  & \left| c \right|=2\times \sqrt{{{\left( \dfrac{-5}{12} \right)}^{2}}+{{\left( -1 \right)}^{2}}} \\
 & \left| c \right|=2\times \sqrt{\dfrac{25}{144}+1} \\
 & =2\times \sqrt{\dfrac{169}{144}} \\
 & =2\times \dfrac{13}{12} \\
 & =\dfrac{13}{6}
\end{align} $
Therefore, the value is $ \left| c \right|=\dfrac{13}{6} $ ,
Taking the modulus out we get,
 $ c=\dfrac{13}{6},\dfrac{-13}{6} $ .
Substituting the values in equation (iii) we get,
 $ y=\dfrac{-5}{12}x+\dfrac{13}{6} $ and $ y=\dfrac{-5}{12}x-\dfrac{13}{6} $
Simplifying we get,
 $ 5x+12y=26 $ and $ 5x+12y=-26 $ .
Plotting the diagrams all the figure, we get,

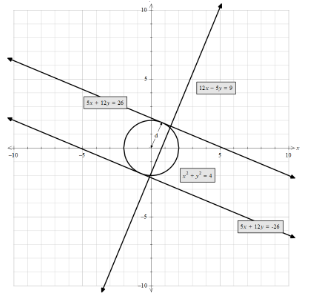
Hence, the equation of the tangents to the circle $ {{x}^{2}}+{{y}^{2}}=4 $ which are perpendicular to the line $ 12x-5y+9=0 $ .

Note: We need to consider both the solutions of the value of c as we open the modulus sign as there will be two pairs of tangents satisfying the same condition. Also, the radius is always perpendicular to the tangent of the circle hence, we can use the formula for the distance of the between the centre and the tangent to the circle. As we can see in the diagram that the point of intersection of the two lines and the point of tangent are not the same. Also, the two values of see give the two lines one above the circle and one below the circle.