Question

Find the equation of the parabola which is symmetric about the y-axis and passes through the point (3, -9).

Answer 1

Hint: We solve this by finding where the points (3, -9) lie in the equation of parabola. Since the parabola is symmetric about the y-axis is \[{x^2} = 4ay\] or \[{x^2} = - 4ay\] . By using the given points (3, -9) we can find the value of ‘a’ and substituting in the required equation we will get the equation of parabola.

Complete step-by-step answer:
We know the equation of parabola about the y-axis is \[{x^2} = 4ay\] or \[{x^2} = - 4ay\] .
Since the points (3, -9) lie in the fourth quadrant so the equation of parabola about the y-axis is \[{x^2} = - 4ay\] . See the below diagram you will understand easily.

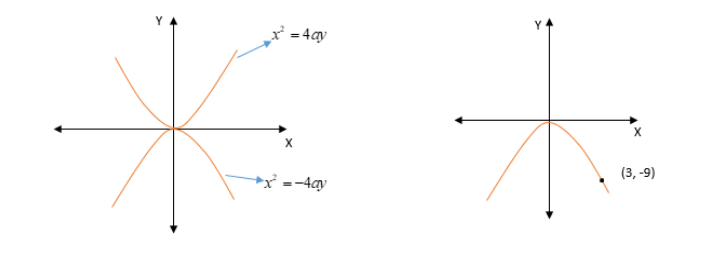
Hence, the equation of parabola is \[{x^2} = - 4ay\] . ---- (1)
We need to find the value of ‘a’.
Now parabola passes through (3, -9), put \[x = 3\] and \[y = - 9\] in equation (1). We get:
 \[ \Rightarrow {3^2} = - 4 \times a \times ( - 9)\]
 \[ \Rightarrow 9 = - 4 \times a \times ( - 9)\]
We know the product of negative and negative is positive and rearranging the above equation we get:
 \[ \Rightarrow a = \dfrac{9}{{9 \times 4}}\]
 \[ \Rightarrow a = \dfrac{1}{4}\]
We know the value of ‘a’. Now substituting in the equation (1). We get
 \[ \Rightarrow {x^2} = - 4\left( {\dfrac{1}{4}} \right)y\]
Cancelling 4,
 \[ \Rightarrow {x^2} = - y\]
 \[ \Rightarrow {x^2} + y = 0\] Is the required equation.
The equation of the parabola which is symmetric about the y-axis and passes through the point (3, -9) is \[{x^2} + y = 0\] .
So, the correct answer is “ \[{x^2} + y = 0\] ”.

Note: If they ask the same question with the same points with a symmetric about the x-axis then we have the equation of parabola is \[{y^2} = 4ax\] or \[{y^2} = - 4ax\] . Follow the same procedure as above you will get the equation of parabola. Careful about the points where it lies (quadrant). Remember the equations of parabola about x-axis and y-axis.