Question

Find the equation of the locus of the point whose distance from the $\text{x-axis}$ is twice that of from the $\text{y-axis}$.
A. \[{{y}^{2}}=4{{x}^{2}}\]
B. \[4{{y}^{2}}={{x}^{2}}\]
C. $\left| y \right|=2\left| x \right|$
D. $4x+y=0$

Answer 1

Hint: First we will start by defining what a locus is and then we will assume a point and then put it into the condition given in the question that is the distance from the $\text{x-axis}$ is twice that of from the $\text{y-axis}$and then plot it in the graph and hence, get the answer.

Complete step by step answer:
Let’s define what a definition of locus is. A locus is a set of points, in geometry, which satisfies a given condition or situation for a shape or a figure. The plural of the locus is loci. The area of the loci is called the region. Now, the locus of points defines a shape in geometry. For example, a circle is the locus of all the points which are at equidistant from the centre. Similarly, the other shapes such as an ellipse, parabola, hyperbola, etc. are defined by the locus of the points. The locus is defined only for curved shapes. These shapes can be regular or irregular. Locus is not described for the shapes having vertex or angles inside them.
Now, we are given to find the equation of the locus of the point whose distance from the $\text{x-axis}$ is twice that of from the $\text{y-axis}$,
Now, let the point be \[P\left( x,y \right)\] , now we know that the distance of the point from $\text{x-axis}$ is: ${{d}_{x}}=\left| y \right|\text{ }..........\text{Equation }\left( 1 \right)$
Similarly, its distance from the $\text{y-axis}$ is: ${{d}_{y}}=\left| x \right|\text{ }..........\text{Equation }\left( 2 \right)$
It is given that the point’s distance from the $\text{x-axis}$ is twice that of from the $\text{y-axis}$,
Therefore: \[{{d}_{x}}=2{{d}_{y}}\] , now we will put values from equation 1 and equation 2:
$\Rightarrow \left| y \right|=2\left| x \right|$

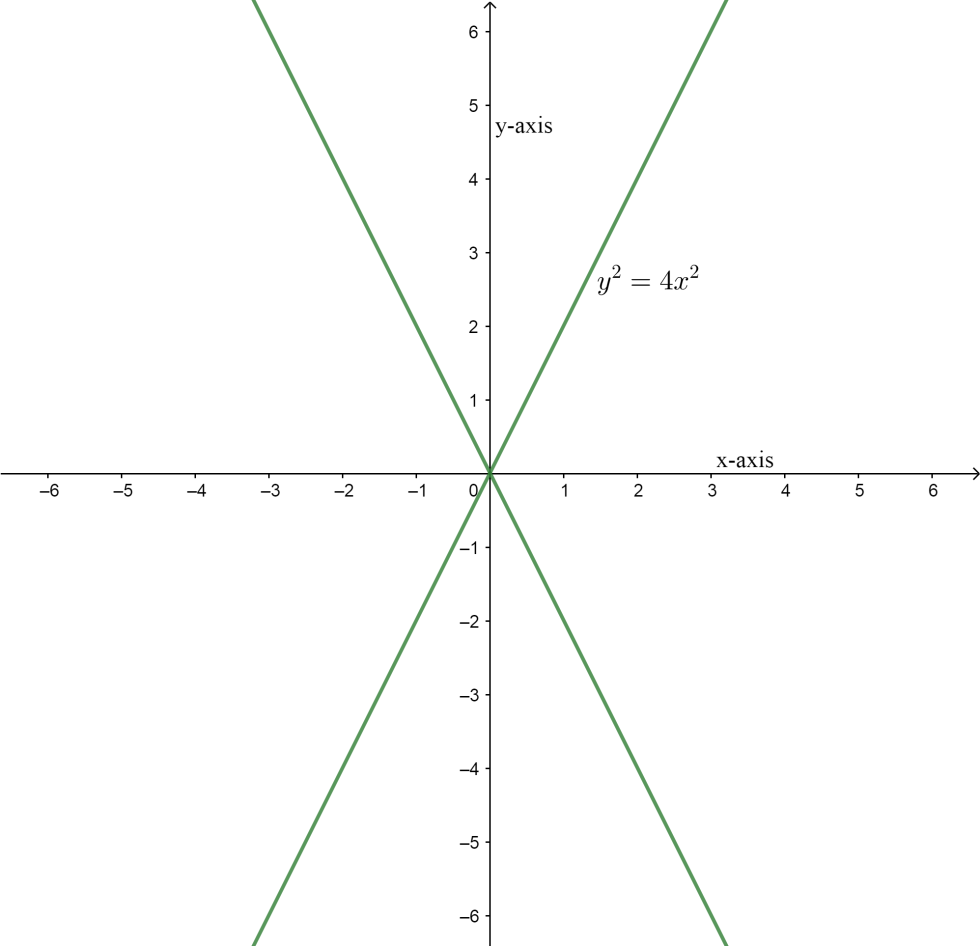
So, the correct answer is “Option C”.

Note: We can also do this question by plotting the points according to the given conditions that is $\left| y \right|=2\left| x \right|$ , let’s see by plotting $P\left( x,y \right)$ for different values in the graph:

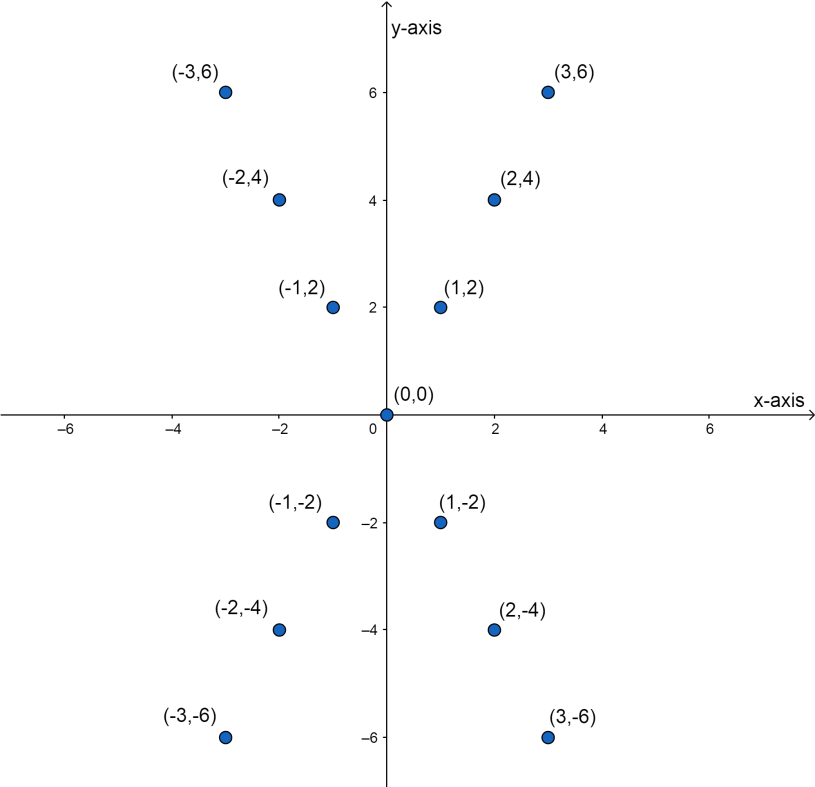
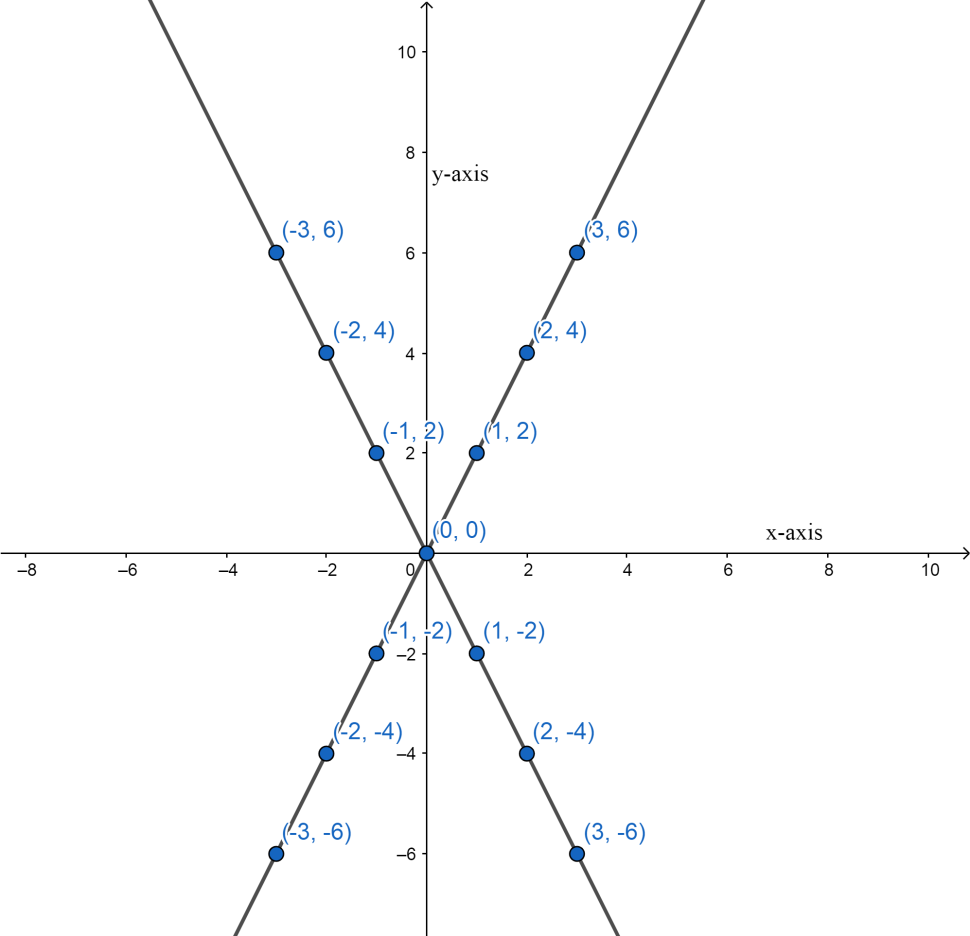
After that we will join all the points and find out the equation of the lines we get and get the locus, therefore: