Question

How do you find the equation of the line tangent to the graph of $f\left( x \right)={{x}^{2}}+5x$. at $x=4$?

Answer 1

Hint: In this question we have to find the equation of a line which is tangent to the given graph. We will first substitute the value of $x=4$ in the given function to get the point $\left( {{x}_{1}},{{y}_{1}} \right)$. we will then find the slope $m$ of the tangent by using the limit function. we will then use the slope-intercept form $y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$ and rearrange to get the required equation of the tangent.

Complete step-by-step answer:
We have the function given to us $f\left( x \right)={{x}^{2}}+5x$.
On substituting $x=4$ in in the function, we get:
$\Rightarrow f\left( 4 \right)={{\left( 4 \right)}^{2}}+5\left( 4 \right)$
On simplifying, we get:
$\Rightarrow f\left( 4 \right)=16+20$
On adding the terms, we get:
$\Rightarrow f\left( 4 \right)=36$
Therefore, the point is $\left( {{x}_{1}},{{y}_{1}} \right)=\left( 4,36 \right)$.
Now we know that the slope of the tangent line to a graph of a given function $f$ at $x=a$ is given by the limit $\displaystyle \lim_{h \to 0}\dfrac{f\left( a+h \right)-f\left( a \right)}{h}$
So, in this question, we have $f\left( x \right)={{x}^{2}}+5x$ and $a=4$, so the slope of the tangent line can be calculated as:
$\Rightarrow \displaystyle \lim_{h \to 0}\dfrac{f\left( 4+h \right)-f\left( 4 \right)}{h}$
On substituting the function, we get:
$\Rightarrow \displaystyle \lim_{h \to 0}\dfrac{\left( {{\left( 4+h \right)}^{2}}+5\left( 4+h \right) \right)-\left( {{\left( 4 \right)}^{2}}+5\left( 4 \right) \right)}{h}$
On simplifying the terms, we get:
$\Rightarrow \displaystyle \lim_{h \to 0}\dfrac{16+8h+{{h}^{2}}+20+5h-\left( 16+20 \right)}{h}$
On simplifying the bracket, we get:
$\Rightarrow \displaystyle \lim_{h \to 0}\dfrac{16+8h+{{h}^{2}}+20+5h-16-20}{h}$
On simplifying, we get:
$\Rightarrow \displaystyle \lim_{h \to 0}\dfrac{8h+{{h}^{2}}+5h}{h}$
On adding the similar terms, we get:
$\Rightarrow \displaystyle \lim_{h \to 0}\dfrac{13h+{{h}^{2}}}{h}$
Now on taking $h$ common in the numerator, we get:
$\Rightarrow \displaystyle \lim_{h \to 0}\dfrac{h\left( 13+h \right)}{h}$
Now since $h \to 0$ and $h\ne 0$, on cancelling, we get:
$\Rightarrow \displaystyle \lim_{h \to 0}\left( 13+h \right)$
On putting the value of $h$, we get:
$\Rightarrow 13$, which is the slope of the tangent line therefore $m=13$.
Now to find the equation of the tangent, we will use the slope intercept form as:
$\Rightarrow y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$
On substituting $\left( {{x}_{1}},{{y}_{1}} \right)$ as $\left( 4,36 \right)$ and $m=13$, we get:
$\Rightarrow y-36=13\left( x-4 \right)$
On simplifying and rearranging the terms, we get:
$\Rightarrow y=13x-16$, which is the required equation for the tangent.
On drawing the function and the tangent on the graph, we get:

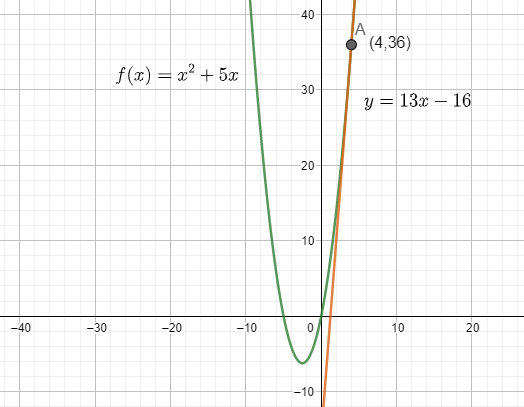
Which is the required solution.

Note: It is to be remembered that a tangent is a line segment which touches the given other curve on the graph through a point. The slope of the line $m$ tells us the steepness of the line. Slope of the line is also called the gradient of the line. It is to be remembered in limits that $h$ should not be substituted in the denominator such that $0$ is present in the denominator.