Question

Find the equation of the curve in Cartesian form \[x=-1+2\sin \theta ,y=1+2\cos \theta .\] Then find the centre and radius of the circle.

Answer 1

Hint: To solve this question, we will calculate x + 1 and y – 1 then calculate the square of them using the formula \[{{\left( a+b \right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}\] and \[{{\left( a-b \right)}^{2}}={{a}^{2}}-2ab+{{b}^{2}}.\] Finally, we will add them to get an equation of the form \[a{{x}^{2}}+b{{y}^{2}}+2hxy+2gx+2fy+c=0\] then the centre \[\left( \dfrac{-g}{a},\dfrac{-f}{a} \right)\] and radius is \[\dfrac{1}{a}\sqrt{{{g}^{2}}+{{f}^{2}}-ac}.\]

Complete step-by-step answer:
We are given
\[x=-1+2\sin \theta .....\left( i \right)\]
\[y=1+2\cos \theta .....\left( ii \right)\]
Consider equation (i), first, we have,
\[x=-1+2\sin \theta \]
\[\Rightarrow x+1=2\sin \theta \]
Squaring both the sides of the above equation, we get,
\[\Rightarrow {{\left( x+1 \right)}^{2}}={{\left( 2\sin \theta \right)}^{2}}\]
\[\Rightarrow {{\left( x+1 \right)}^{2}}=4{{\sin }^{2}}\theta \]
Using the identity of the square of two numbers given as
\[{{\left( a+b \right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}\]
Using this in \[{{\left( x+1 \right)}^{2}}\] we have
\[{{\left( x+1 \right)}^{2}}={{x}^{2}}+2x+1\]
\[\Rightarrow {{\left( x+1 \right)}^{2}}=4{{\sin }^{2}}\theta \]
\[\Rightarrow {{x}^{2}}+2x+1=4{{\sin }^{2}}\theta .....\left( iii \right)\]
Consider the equation (ii) now, we have,
\[y=1+2\cos \theta \]
\[\Rightarrow y-1=2\cos \theta \]
Squaring both the sides of the above equation, we have,
\[\Rightarrow {{\left( y-1 \right)}^{2}}={{\left( 2\cos \theta \right)}^{2}}\]
\[\Rightarrow {{\left( y-1 \right)}^{2}}=4{{\cos }^{2}}\theta \]
Now, we have an identity of the square of the difference of two numbers which is given by \[{{\left( a-b \right)}^{2}}={{a}^{2}}-2ab+{{b}^{2}}.\] Using this identity in \[{{\left( y-1 \right)}^{2}},\] we have,
\[{{\left( y-1 \right)}^{2}}={{y}^{2}}-2y+1\]
\[\Rightarrow {{\left( y-1 \right)}^{2}}=4{{\cos }^{2}}\theta \]
\[\Rightarrow {{y}^{2}}-2y+1=4{{\cos }^{2}}\theta .....\left( iv \right)\]
To get the required equation of the curve, let us add the equation (iii) and equation (iv).
Equation (iii) is \[{{x}^{2}}+2x+1=4{{\sin }^{2}}\theta .\]
Equation (iv) is \[{{y}^{2}}-2y+1=4{{\cos }^{2}}\theta .\]
Adding these, we get,
\[{{x}^{2}}+2x+1+{{y}^{2}}-2y+1=4{{\sin }^{2}}\theta +4{{\cos }^{2}}\theta \]
\[\Rightarrow {{x}^{2}}+2x+{{y}^{2}}-2y+2=4{{\sin }^{2}}\theta +4{{\cos }^{2}}\theta \]
Using \[{{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1,\] we get,
\[\Rightarrow {{x}^{2}}+2x+{{y}^{2}}-2y+2=4\left( {{\sin }^{2}}\theta +{{\cos }^{2}}\theta \right)\]
\[\Rightarrow {{x}^{2}}+2x+{{y}^{2}}-2y+2=4\times 1\]
\[\Rightarrow {{x}^{2}}+2x+{{y}^{2}}-2y+2=4\]
This is the required equation of the curve when \[x=-1+2\sin \theta \] and \[y=1+2\cos \theta .\] This is a 2-degree equation, we have,
\[{{x}^{2}}+{{y}^{2}}+2x-2y+2-4=0\]
\[\Rightarrow {{x}^{2}}+{{y}^{2}}+2x-2y-2=0\]
Finally, we have to find the centre and radius of the circle from the obtained curve.
\[{{x}^{2}}+{{y}^{2}}+2x-2y-2=0.....\left( v \right)\]
The general equation of the second degree is given by
\[a{{x}^{2}}+2hxy+b{{y}^{2}}+2gx+2fy+c=0......\left( vi \right)\]
Here, the centre of the circle is given by \[\left( \dfrac{-g}{a},\dfrac{-f}{a} \right)\] and the radius is given by \[\dfrac{1}{a}\sqrt{{{g}^{2}}+{{f}^{2}}-ac}.\]
So, finally, we will use this to get our result. Let us compare equations (v) and (vi).
\[\Rightarrow a=1;2=2g\]
\[\Rightarrow b=1;2f=-2\]
\[\Rightarrow 2h=0;c=-2\]
\[\Rightarrow a=b=1,h=0,g=1,f=-1,c=-2\]
Then the centre of the circle is given by \[\left( \dfrac{-g}{a},\dfrac{-f}{a} \right)=\left( -1,1 \right).\] And the radius of our curve circle is given by
\[\dfrac{1}{a}\sqrt{{{g}^{2}}+{{f}^{2}}-ac}=\dfrac{1}{1}\sqrt{{{\left( 1 \right)}^{2}}+{{\left( -1 \right)}^{2}}+2}\]
\[\Rightarrow \dfrac{1}{a}\sqrt{{{g}^{2}}+{{f}^{2}}-ac}=\sqrt{4}\]
\[\Rightarrow \dfrac{1}{a}\sqrt{{{g}^{2}}+{{f}^{2}}-ac}=2\]
Hence, the curve is given by \[{{x}^{2}}+{{y}^{2}}+2x-2y-2=0\] and the centre is given by (– 1, 1) and radius = 2.

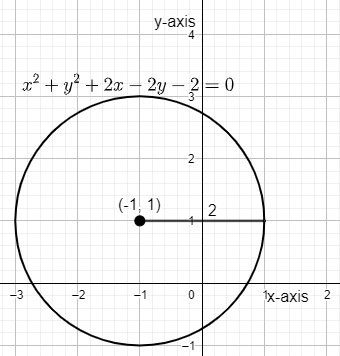
Note: Another method can be simply adding \[{{\left( x+1 \right)}^{2}}\] and \[{{\left( y-1 \right)}^{2}}\] and this gives \[{{\left( x+1 \right)}^{2}}+{{\left( y-1 \right)}^{2}}=4\left( {{\sin }^{2}}\theta +{{\cos }^{2}}\theta \right)=4\times 1=4.\] Then the required equation is \[{{\left( x+1 \right)}^{2}}+{{\left( y-1 \right)}^{2}}={{\left( 2 \right)}^{2}}.\] When the equation of the circle is of the form \[{{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}\] then the centre is (a, b) and the radius = r. Comparing it from \[{{\left( x+1 \right)}^{2}}+{{\left( y-1 \right)}^{2}}={{2}^{2}}\] we have the centre as (– 1, 1) and the radius is 2 which is same as obtained above.