Question

Find the equation of the circumcircle of the triangle formed by the lines $ 5x - 3y + 4 = 0 $ , $ 2x + 3y - 5 = 0 $ , $ x + y = 0 $

Answer 1

Hint: Here it is given that the triangle is formed by the lines $ 5x - 3y + 4 = 0 $ , $ 2x + 3y - 5 = 0 $ , $ x + y = 0 $ . We are asked to calculate the equation of the circumcircle of the triangle formed by the given lines.
Let AB denote the line equation $ 5x - 3y + 4 = 0 $ , BC denote the line $ 2x + 3y - 5 = 0 $ and AC denote the line equation $ x + y = 0 $ . We need to solve these equations to obtain the vertices of the given triangle.
Formula to be used:
The general equation of the circle is\[{x^2} + {y^2} + 2gx + 2fy + c = 0\]

Complete step by step answer:
It is given that the triangle is formed by the lines $ 5x - 3y + 4 = 0 $ , $ 2x + 3y - 5 = 0 $ , $ x + y = 0 $ . We are asked to calculate the equation of the circumcircle of the triangle formed by the given lines.
We need to solve these equations to obtain the vertices of the given triangle.
Let\[AB \Rightarrow 5x - 3y + 4 = 0\] …….. $ \left( 1 \right) $
\[BC \Rightarrow 2x + 3y - 5 = 0\] ……………… $ \left( 2 \right) $
\[CA \Rightarrow x + y = 0\;\] ………….. $ \left( 3 \right) $

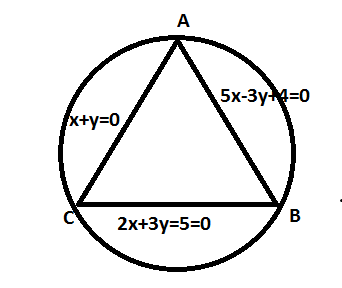
To obtain point A, we shall solve the equations $ \left( 1 \right) $ and $ \left( 3 \right) $ .
From $ \left( 1 \right) $ , we have
 $ 5x = 3y - 4 $
 $ \Rightarrow x = \dfrac{{3y - 4}}{5} $ ……… $ \left( 4 \right) $
We shall substitute $ \left( 4 \right) $ in $ \left( 3 \right) $ .
That is $ x + y = 0 \Rightarrow \dfrac{{3y - 4}}{5} + y = 0 $
 $ \Rightarrow \dfrac{{3y - 4 + 5y}}{5} = 0 $
 $ \Rightarrow 3y - 4 + 5y = 0 $
 $ \Rightarrow 8y = 4 $
 $ \Rightarrow y = \dfrac{1}{2} $
Now, we shall substitute the above result in $ \left( 4 \right) $ .
 $ x = \dfrac{{3y - 4}}{5} \Rightarrow x = \dfrac{{3 \times \dfrac{1}{2} - 4}}{5} $
 $ \Rightarrow x = \dfrac{1}{5} \times \dfrac{{3 - 8}}{2} $
 $ \Rightarrow x = \dfrac{1}{5} \times \dfrac{{ - 5}}{2} $
 $ \Rightarrow x = \dfrac{{ - 1}}{2} $
Hence, the required point is $ A\left( { - \dfrac{1}{2},\dfrac{1}{2}} \right) $
To obtain point B, we shall solve the equations $ \left( 1 \right) $ and $ \left( 2 \right) $ .
Adding $ \left( 1 \right) $ and $ \left( 2 \right) $ , we have
 $ 5x - 3y + 4 + 2x + 3y - 5 = 0 $
 $ \Rightarrow 7x - 1 = 0 $
\[ \Rightarrow x = \dfrac{1}{7}\]
Now, we shall substitute the above result in $ \left( 1 \right) $
 $ 5x - 3y + 4 = 0 \Rightarrow \dfrac{5}{7} - 3y + 4 = 0 $
 $ \Rightarrow \dfrac{{5 - 21y + 28}}{7} = 0 $
 $ \Rightarrow \dfrac{{ - 21y + 33}}{7} = 0 $
 $ \Rightarrow - 21y = - 33 $
 $ \Rightarrow y = \dfrac{{33}}{{21}} $
 $ \Rightarrow y = \dfrac{{11}}{7} $
Hence, the required point is $ B\left( {\dfrac{1}{7},\dfrac{{11}}{7}} \right) $
To obtain point C, we shall solve the equations $ \left( 2 \right) $ and $ \left( 3 \right) $ .
From $ \left( 3 \right) $ , we have
 $ x + y = 0 $
 $ \Rightarrow x = - y $ ……… $ \left( 5 \right) $
We shall substitute $ \left( 4 \right) $ in $ \left( 2 \right) $ .
That is $ 2x + 3y - 5 = 0 \Rightarrow 2 \times - y + 3y - 5 = 0 $
 $ \Rightarrow - 2y + 3y - 5 = 0 $
 $ \Rightarrow y = 5 $
Now, we shall the above result in $ \left( 5 \right) $ .
 $ x = - y \Rightarrow x = - 5 $
 $ \Rightarrow x = - 5 $
Hence, the required point is $ C\left( { - 5,5} \right) $
Now, we obtained three points A, B, and C. We need to substitute the points on the equation of the circle one by one.
The general equation of the circle is\[{x^2} + {y^2} + 2gx + 2fy + c = 0\]……….. $ \left( 6 \right) $
We shall substitute the point $ A\left( { - \dfrac{1}{2},\dfrac{1}{2}} \right) $ in $ \left( 6 \right) $ .
That is \[{\left( {\dfrac{1}{2}} \right)^2} + {\left( {\dfrac{1}{2}} \right)^2} - 2g \times \dfrac{1}{2} + 2f \times \dfrac{1}{2} + c = 0\]
\[ \Rightarrow \dfrac{1}{4} + \dfrac{1}{4} - g + f + c = 0\] ……………. $ \left( 7 \right) $
 We shall substitute the point $ B\left( {\dfrac{1}{7},\dfrac{{11}}{7}} \right) $ in $ \left( 6 \right) $ .
That is \[{\left( {\dfrac{1}{7}} \right)^2} + {\left( {\dfrac{{11}}{7}} \right)^2} + 2g \times \dfrac{1}{7} + 2f \times \dfrac{{11}}{7} + c = 0\]
\[ \Rightarrow \dfrac{1}{{49}} + \dfrac{{121}}{{49}} + \dfrac{{2g}}{7} + \dfrac{{22f}}{7} + c = 0\] ……………. $ \left( 8 \right) $
We shall substitute the point $ C\left( { - 5,5} \right) $ in $ \left( 6 \right) $ .
That is \[{\left( { - 5} \right)^2} + {5^2} + 2g \times - 5 + 2f \times 5 + c = 0\]
\[ \Rightarrow 25 + 25 - 10g + 10f + c = 0\]
\[ \Rightarrow - 10g + 10f + c = - 50\] ……………. $ \left( 9 \right) $
Now, we shall subtract $ \left( 7 \right) $ and $ \left( 9 \right) $
\[ \Rightarrow \dfrac{1}{4} + \dfrac{1}{4} - g + f + c + 10g - 10f - c = 50\]
\[ \Rightarrow 9g - 9f = 50 - \dfrac{1}{2}\]
\[ \Rightarrow 9g - 9f = \dfrac{{100 - 1}}{2}\]
\[ \Rightarrow g - f = \dfrac{{99}}{2} \times \dfrac{1}{9}\]
\[ \Rightarrow g - f = \dfrac{{11}}{2}\] ……….. $ \left( {10} \right) $
Now, we shall subtract $ \left( 7 \right) $ and $ \left( 8 \right) $
\[ \Rightarrow \dfrac{1}{4} + \dfrac{1}{4} - g + f + c - \dfrac{1}{{49}} - \dfrac{{121}}{{49}} - \dfrac{{2g}}{7} - \dfrac{{22f}}{7} - c = 0\]
\[ \Rightarrow - g - \dfrac{{2g}}{7} + f - \dfrac{{22f}}{7} + \dfrac{1}{2} - \dfrac{{122}}{{49}} = 0\]
\[ \Rightarrow \dfrac{{ - 7g - 2g}}{7} + \dfrac{{ + 7f - 22f}}{7} + \dfrac{{49 - 244}}{{2 \times 49}} = 0\]
\[ \Rightarrow \dfrac{{ - 9g}}{7} + \dfrac{{ - 15f}}{7} + \dfrac{{ - 195}}{{49 \times 2}} = 0\]
\[ \Rightarrow - 3\left( {\dfrac{{3g}}{7} + \dfrac{{5f}}{7} + \dfrac{{65}}{{49 \times 2}}} \right) = 0\]
\[ \Rightarrow \dfrac{1}{7}\left( {3g + 5f + \dfrac{{65}}{{14}}} \right) = 0\]
\[ \Rightarrow 3g + 5f = - \dfrac{{65}}{{14}}\] …………… $ \left( {11} \right) $
Now, we shall solve $ \left( {10} \right) $ and $ \left( {11} \right) $ .
That is multiply $ \left( {10} \right) $ by $ 5 $ and add $ \left( {10} \right) $ and $ \left( {11} \right) $
\[ \Rightarrow 5g - 5f + 3g + 5f = \dfrac{{55}}{2} - \dfrac{{65}}{{14}}\]
\[ \Rightarrow 8g = \dfrac{{385 - 65}}{{14}}\]
\[ \Rightarrow 8g = \dfrac{{320}}{{14}}\]
\[ \Rightarrow g = \dfrac{{320}}{{14}} \times \dfrac{1}{8}\]
\[ \Rightarrow g = \dfrac{{40}}{{14}}\]
Now, substitute the above result in $ \left( {10} \right) $
\[g - f = \dfrac{{11}}{2} \Rightarrow \dfrac{{40}}{{14}} - f = \dfrac{{11}}{2}\]
\[ \Rightarrow \dfrac{{40}}{{14}} - \dfrac{{11}}{2} = f\]
\[ \Rightarrow \dfrac{{40 - 77}}{{14}} = f\]
 $ \Rightarrow f = - \dfrac{{37}}{{14}} $
Now, substitute the value of g and f in $ \left( 7 \right) $
That is\[ \Rightarrow \dfrac{1}{4} + \dfrac{1}{4} - g + f + c = 0 \Rightarrow \dfrac{1}{4} + \dfrac{1}{4} - \dfrac{{40}}{{14}} + \dfrac{{ - 37}}{{14}} + c = 0\]
\[ \Rightarrow \dfrac{1}{2} - \dfrac{{40}}{{14}} + \dfrac{{ - 37}}{{14}} + c = 0\]
\[ \Rightarrow \dfrac{{7 - 40 - 37}}{{14}} + c = 0\]
\[ \Rightarrow \dfrac{{ - 70}}{{14}} + c = 0\]
\[ \Rightarrow c = \dfrac{{70}}{{14}}\]
At last, substitute the values of g, f, and c in $ \left( 6 \right) $
\[{x^2} + {y^2} + 2 \times \dfrac{{40}}{{14}}x + 2 \times \dfrac{{ - 37}}{{14}}y + \dfrac{{70}}{{14}} = 0\]
 $ \Rightarrow {x^2} + {y^2} + \dfrac{{40}}{7}x + \dfrac{{ - 37}}{7}y + 5 = 0 $
 $ \Rightarrow 7{x^2} + 7{y^2} + 40x - 37y + 35 = 0 $
Hence, the required equation of the circle is $ 7{x^2} + 7{y^2} + 40x - 37y + 35 = 0 $

Note: We assumed that AB denotes the line equation $ 5x - 3y + 4 = 0 $ , BC denotes the line $ 2x + 3y - 5 = 0 $ and AC denotes the line equation $ x + y = 0 $ . We have solved these equations to obtain the vertices of the given triangle.
Hence, the required equation of the circle is $ 7{x^2} + 7{y^2} + 40x - 37y + 35 = 0 $