Question

Find the equation of the circle passing through $ \left( 0,0 \right) $ and making intercepts $ a $ and $ b $ on the coordinate axes.

Answer 1

Hint: We denote the centre of the circle as $ C\left( h,k \right) $ and radius $ OA=r $ where O is the origin. We use given intercepts $ a,b $ and find the coordinates of $ A,B $ where $ x- $ and $ y- $ axis cut the circle excluding O. We put the coordinates of $ A,B,O $ in the equation of the circle in centre-radius to express $ h,k,{{r}^{2}} $ in terms of $ a,b $ . We put the expressions in $ a,b $ centre-radius equation of circle to get the required.

Complete step-by-step answer:
Let us denote the centre of the given circle in the question as $ C\left( h,k \right) $ and the radius as $ OA=r $ where O is the origin. Let $ x- $ axis cut circle excluding the origin at A and $ y- $ axis cut circle excluding the origin at B . So we have obtained the $ x- $ intercept OA and $ y- $ intercept OB. We are given i the question that $ a $ and $ b $ are length of the intercept. We assign
\[OA=a,OB=b\]
So the co-ordinates of A and B are given by $ A\left( a,0 \right),B\left( 0,b \right) $ . \[\]

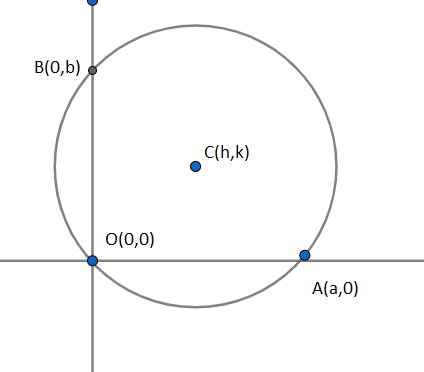
We write the equation of the circle in centre radius form as
\[{{\left( x-h \right)}^{2}}+{{\left( y-k \right)}^{2}}={{r}^{2}}......\left( 1 \right)\]
The circle (1) passes through origin $ O\left( 0,0 \right) $ and so $ O\left( 0,0 \right) $ will satisfy equation of circle (1). So we have,
\[\begin{align}
  & {{\left( 0-h \right)}^{2}}+{{\left( 0-k \right)}^{2}}={{r}^{2}}. \\
 & \Rightarrow {{h}^{2}}+{{k}^{2}}={{r}^{2}}......\left( 2 \right) \\
\end{align}\]
The circle (1) passes through origin $ A\left( a,0 \right) $ and so $ A\left( a,0 \right) $ will satisfy equation of circle (1). So we have,
\[\begin{align}
  & {{\left( a-h \right)}^{2}}+{{\left( 0-k \right)}^{2}}={{r}^{2}}. \\
 & \Rightarrow {{a}^{2}}-2ah+{{h}^{2}}+{{k}^{2}}={{r}^{2}} \\
 & \Rightarrow {{a}^{2}}-2ah+{{r}^{2}}={{r}^{2}}\left( \because {{h}^{2}}+{{k}^{2}}={{r}^{2}} \right) \\
 & \Rightarrow a\left( a-2h \right)=0 \\
\end{align}\]
So we have $ a=0 $ or $ h=\dfrac{a}{2} $ . If $ a=0 $ the point is on $ x- $ axis and we reject the value. So the $ x- $ coordinate of the centre is $ h=\dfrac{a}{2} $ .
The circle (1) passes through origin $ B\left( 0,b \right) $ and so $ A\left( 0,b \right) $ will satisfy equation of circle (1). So we have,
\[\begin{align}
  & {{\left( 0-h \right)}^{2}}+{{\left( b-k \right)}^{2}}={{r}^{2}}. \\
 & \Rightarrow {{h}^{2}}+{{b}^{2}}-2kb+{{k}^{2}}={{r}^{2}} \\
 & \Rightarrow {{b}^{2}}-2kb+{{r}^{2}}={{r}^{2}}\left( \because {{h}^{2}}+{{k}^{2}}={{r}^{2}} \right) \\
 & \Rightarrow b\left( b-2k \right)=0 \\
\end{align}\]
So we have $ b=0 $ or $ k=\dfrac{b}{2} $ . If $ b=0 $ the point is on $ y- $ axis and we reject the value. So the $ y- $ coordinate of the centre is $ k=\dfrac{b}{2} $ . Let us put the value of $ h=\dfrac{a}{2},k=\dfrac{b}{2} $ in the equation (2) and find $ {{r}^{2}} $ . We have
\[\begin{align}
  & {{\left( \dfrac{a}{2} \right)}^{2}}+{{\left( \dfrac{b}{2} \right)}^{2}}={{r}^{2}} \\
 & \Rightarrow {{r}^{2}}=\dfrac{{{a}^{2}}+{{b}^{2}}}{4} \\
\end{align}\]
 We put the obtained values of $ h,k,{{r}^{2}} $ in equation(1) and have
\[\begin{align}
  & {{\left( x-\dfrac{a}{2} \right)}^{2}}+{{\left( y-\dfrac{b}{2} \right)}^{2}}=\dfrac{{{a}^{2}}+{{b}^{2}}}{4} \\
 & \Rightarrow {{x}^{2}}-ax+\dfrac{{{a}^{2}}}{4}+{{y}^{2}}-bx+\dfrac{{{b}^{2}}}{4}=\dfrac{{{a}^{2}}+{{b}^{2}}}{4} \\
 & \Rightarrow {{x}^{2}}-ax+{{y}^{2}}-bx+\dfrac{{{a}^{2}}+{{b}^{2}}}{4}=\dfrac{{{a}^{2}}+{{b}^{2}}}{4} \\
 & \Rightarrow {{x}^{2}}-ax+{{y}^{2}}-bx=0 \\
\end{align}\]
The above equation is the required equation of the circle. \[\]

Note: We can also proceed to find the equation of the circle with $ x- $ intercept as $ b $ and h $ y- $ intercept as $ a $ and get the equation as $ {{x}^{2}}-bx+{{y}^{2}}-ay=0 $ . The general equation of circle in two variables is given by $ {{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0 $ for real numbers $ f,g,c $ which simultaneously cannot be zero and $ {{g}^{2}}+{{f}^{2}} > c $ .