Question

Find the equation of the circle of minimum radius which contains the three circles
\[
  {S_1} \equiv {x^2} + {y^2} - 4y - 5 = 0 \\
  {S_2} \equiv {x^2} + {y^2} + 12x + 4y + 31 = 0 \\
  {S_3} \equiv {x^2} + {y^2} + 6x + 12y + 36 = 0 \\
 \]

Answer 1

Hint: The center through which the circle of different radii has been drawn is known as the circumcentre of those circles. Find the radius and the centers of the circles and draw a circle passing through the radius of the three circles with circumcentre being the center. Then, find the center and the distance from the center of the circle of the other three circles for radius.

Complete step by step answer:
 The general form of the equation of the circle\[{x^2} + {y^2} + 2gx + 2fy + c = 0\], where the center of the circle is\[\left( { - g, - f} \right)\], and the radius is \[\sqrt {\left( {{g^2} + {f^2} - c} \right)} \]

$\Rightarrow$ For the equation \[{S_1} \equiv {x^2} + {y^2} - 4y - 5 = 0\] of the circle, we get to the center, \[{C_1} = \left( {0,2} \right)\] radius \[{r_1} = 3\]

$\Rightarrow$ For the equation \[{S_2} \equiv {x^2} + {y^2} + 12x + 4y + 31 = 0\] of the circle, we get to the center, \[{C_2} = \left( { - 6, - 2} \right)\]and radius \[{r_2} = 3\]

$\Rightarrow$ For the equation \[{S_3} \equiv {x^2} + {y^2} + 6x + 12y + 36 = 0\] of the circle, we get to the center, \[{C_3} = \left( { - 3, - 6} \right)\] and radius \[{r_3} = 3\]

From the given three circle equations we can observe circles have the same radius \[r = 3\]

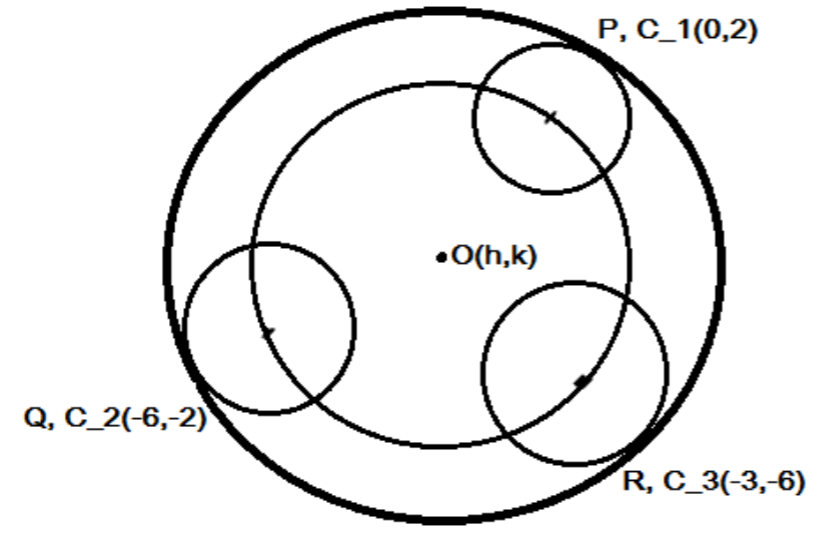
In the above diagram, the radius of the circle touches all the circles represented by:
$\Rightarrow$ \[CP = C{C_1} + {C_1}P = C{C_1} + 3 = C{C_2} + 3 = C{C_3} + 3\]
Let us assume \[C(h,k)\]to be the center of the required circle.
Then, \[C{C_1} = C{C_2} = C{C_3}\] or \[CC_{_1}^2 = CC_{_2}^2 = CC_3^2\]
We get the equation as:
$\Rightarrow$ \[{(h - 0)^2} + {(k - 2)^2} = {(h + 6)^2} + {(k + 2)^2} = {(h + 3)^2} + {(k + 6)^2}\]
$\Rightarrow$ Applying, the arithmetic identity, ${\left( {a + b} \right)^2} = {a^2} + 2ab + {b^2}$ in the equation (i) as:
\[
 \Rightarrow \left( {{h^2}} \right) + \left( {{k^2} - 4k + 4} \right) = \left( {{h^2} + 12h + 36} \right) + \left( {{k^2} + 4k + 4} \right) = \left( {{h^2} + 6h + 9} \right) + \left( {{k^2} + 12k + 36} \right) \\
 \Rightarrow \left( {{h^2} + {k^2}} \right) - 4k + 4 = \left( {{h^2} + {k^2}} \right) + 12h + 4k + 40 = \left( {{h^2} + {k^2}} \right) + 6h + 12k + 45 \\
 \Rightarrow - 4k + 4 = 12h + 4k + 40 = 6h + 12k + 45 \\
 \]
 By equating pair of equations we get:
$\Rightarrow$ \[6h + 16k + 41 = 0\]-- (i)
$\Rightarrow$ And \[6h - 8k - 5 = 0\]--(ii)
From equation (i)
\[
\Rightarrow 6h + 16k + 41 = 0 \\
\Rightarrow 6h = - 16k - 41 \\
\Rightarrow h = \dfrac{{ - 16k - 41}}{6} - - - - (iii) \\
 \]
Substitute the value of h from equation (iii) in equation (ii), we get
\[
 \Rightarrow 6h - 8k - 5 = 0 \\
\Rightarrow 8k = 6h - 5 \\
\Rightarrow 8k = 6\left( {\dfrac{{ - 16k - 41}}{6}} \right) - 5 \\
 \Rightarrow 8k = - 16k - 46 \\
 \Rightarrow 24k = - 46 \\
 \Rightarrow k = - \dfrac{{46}}{{24}} = - \dfrac{{23}}{{12}} \\
 \]
Solving for the value of \[h\] we get:
\[
\Rightarrow h = \dfrac{{ - 16k - 41}}{6} \\
\Rightarrow 6h = - 16\left( { - \dfrac{{23}}{{12}}} \right) - 41 \\
\Rightarrow 6h = \dfrac{{4 \times 23}}{3} - 41 \\
\Rightarrow 18h = 92 - 123 \\
\Rightarrow h = - \dfrac{{31}}{{18}} \\
 \]
Hence, by solving equation (i) and (ii) we get \[h = \dfrac{{ - 31}}{{18}}\] and \[k = \dfrac{{ - 23}}{{12}}\]
Now we will find the radius of the required circle by substituting the value of h and k in the equation $\Rightarrow$ $C{C_1} = \sqrt {{{\left( {0 + h} \right)}^2} + {{\left( {2 + k} \right)}^2}} $ as:
$\Rightarrow$ \[C{C_1} = \sqrt {{{\left( {0 + \dfrac{{31}}{{18}}} \right)}^2} + {{\left( {2 + \dfrac{{23}}{{12}}} \right)}^2}} = \dfrac{5}{{36}}\sqrt {949} \]
Since, \[CP = C{C_1} + 3 = \dfrac{5}{{36}}\sqrt {949} + 3\]
The radius of the required circle is \[CP = \dfrac{5}{{36}}\sqrt {949} + 3\]
Hence the required equation of the circle is:
 \[
\Rightarrow {\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {r^2} \\
\Rightarrow {\left( {x + \dfrac{{31}}{{18}}} \right)^2} + {\left( {y + \dfrac{{23}}{{12}}} \right)^2} = {\left( {\dfrac{5}{{39}}\sqrt {949} + 3} \right)^2} \\
 \]

Note: In general, when the question is about to find the circle on which all circles lie, we need to find the circumcentre of the circle. Alternatively, circumcentre can be found by considering a general equation of the circle and solving all the equations with the variables of the circumcentre to be determined.