Question

Find the equation of the circle concentric with the circle ${x^2} + {y^2} - 8x + 6y - 5 = 0$ and passing through the point $\left( { - 2, - 7} \right)$

Answer 1

Hint: Concentric circles have the same centre. So compare the given circle equation with the general form of circle equation ${x^2} + {y^2} + 2gx + 2fy + c = 0$ and get the values of g and f. The coordinates of the centre of a circle are (-g,-f). Find the centre and this centre is the same for the required circle. It is given that the required circle passes through $\left( { - 2, - 7} \right)$. So to find the radius find the distance between the given point and centre. Find the new equation of circle by substituting r, h, k in ${\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {r^2}$ where (h, k) are the coordinates of the centre.

Complete step-by-step answer:
We are given an equation of a circle ${x^2} + {y^2} - 8x + 6y - 5 = 0$
We have to find the equation of another circle which is concentric with the above circle and passes through $\left( { - 2, - 7} \right)$

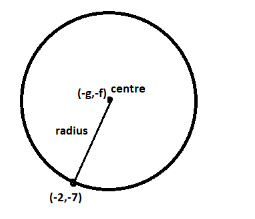
Concentric circles have the same centre so find the centre of the given circle.
On comparing ${x^2} + {y^2} - 8x + 6y - 5 = 0$ with ${x^2} + {y^2} + 2gx + 2fy + c = 0$, we get the value of g is -4 and value of f is 3.
Centre is $\left( { - g, - f} \right) = \left( { - \left( { - 4} \right), - 3} \right) = \left( {4, - 3} \right)$

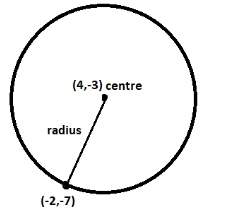
The radius of the required circle will be the distance between centre and $\left( { - 2, - 7} \right)$
Radius is
$
  r = \sqrt {{{\left( {4 - \left( { - 2} \right)} \right)}^2} + {{\left( { - 3 - \left( { - 7} \right)} \right)}^2}} \\
   \to r = \sqrt {{6^2} + {4^2}} = \sqrt {36 + 16} \\
   \to r = \sqrt {52} units \\
 $
The equations of the new circle is ${\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {r^2}$, where r is the radius, (h, k) are the coordinates of centre.
$
  {\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {r^2} \\
  r = \sqrt {52} ,\left( {h,k} \right) = \left( {4, - 3} \right) \\
   \to {\left( {x - 4} \right)^2} + {\left( {y - \left( { - 3} \right)} \right)^2} = {\left( {\sqrt {52} } \right)^2} \\
   \to {\left( {x - 4} \right)^2} + {\left( {y + 3} \right)^2} = 52 \\
   \to {x^2} + 16 - 8x + {y^2} + 9 + 6y = 52 \\
  \left( {\because {{\left( {a + b} \right)}^2} = {a^2} + {b^2} + 2ab,{{\left( {a - b} \right)}^2} = {a^2} + {b^2} - 2ab} \right) \\
   \to {x^2} + {y^2} - 8x + 6y + 25 = 52 \\
   \to {x^2} + {y^2} - 8x + 6y + 25 - 52 = 0 \\
  \therefore {x^2} + {y^2} - 8x + 6y - 27 = 0 \\
 $
Therefore, the equation of the circle is \[{x^2} + {y^2} - 8x + 6y - 27 = 0\]

Note: When you are unsure about the resulting equation whether it is correct or not, just verify it by substituting the given point (x, y) in the solution you got; in the above solution the point is (-2, -7). After substituting the equation must result zero. This ensures that your solution is correct.
$
  {x^2} + {y^2} - 8x + 6y - 27 = 0 \\
  \left( {x,y} \right) = \left( { - 2, - 7} \right) \\
   \to - {2^2} + \left( { - {7^2}} \right) - 8\left( { - 2} \right) + 6\left( { - 7} \right) - 27 = 0 \\
   \to 4 + 49 + 16 - 42 - 27 = 0 \\
   \to 27 - 27 = 0 \\
  \therefore 0 = 0 \\
 $
LHS=RHS, therefore the solution we got is correct.