Question

Find the equation of the altitudes of a triangle ABC, whose vertices are A (2,-2), B (1, 1) and C (-1, 0).

Answer 1

Hint: Altitude of a triangle is referred to as a line segment joining the vertices of the triangle with its opposite side at perpendicular degree. The line to which these altitudes meet is known as extended base and the point of their intersection is called foot of altitude.
To find the equation of the line slope of that line is very necessary which is described as the ratio of change in vertical axis to the change in horizontal axis on a two-dimensional plane represented as\[m = \dfrac{{\Delta y}}{{\Delta x}} = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\].

Complete step by step solution:
In the triangle ABC whose vertices are given as\[A\left( {2, - 2} \right),B\left( {1,1} \right),C\left( { - 1,0} \right)\], let AD be an altitude from the vertex \[A\] perpendicular to the line BC.

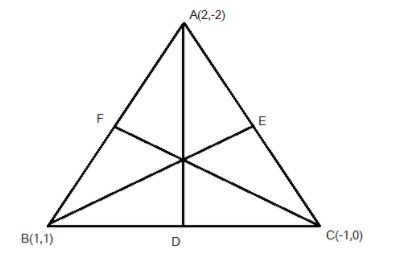
Now let us consider the slope of the line AD and BC be \[{m_1}\]and \[{m_2}\]respectively
As altitude AD is perpendicular to line BC we can say
\[
  {m_1} \times {m_2} = - 1 \\
  {m_1} = - \dfrac{1}{{{m_2}}} \\
 \]
Now find the slope \[{m_2}\]of line BC equal to
\[{m_2} = \dfrac{{{y_c} - {y_b}}}{{x{}_c - {x_b}}} = \dfrac{{0 - 1}}{{ - 1 - 1}} = \dfrac{{ - 1}}{{ - 2}} = \dfrac{1}{2}\]
Now find the slope \[{m_1}\]of the line AD by
\[{m_1} = - \dfrac{1}{{{m_2}}} = - \dfrac{1}{{\dfrac{1}{2}}} = - 2\]
Hence the equation of the line AD originating from vertex A (2, -2) and having slope \[{m_1} = - 2\]will be
\[
  y - {y_a} = {m_1}\left( {x - {x_a}} \right) \\
  y + 2 = \left( { - 2} \right)\left( {x - 2} \right) \\
  y + 2 = - 2x + 4 \\
  y = - 2x + 2 \\
 \]
Finally we get the equation of the altitude AD \[y = - 2x + 2\]
Now let BE be an altitude from vertex perpendicular to the line AC, where \[{m_3}\] and \[{m_4}\] are the slope of the line BE and AC respectively and the lines BE and AC are perpendicular to each other, hence
\[
  {m_3} \times {m_4} = - 1 \\
  {m_3} = - \dfrac{1}{{{m_4}}} \\
 \]
Now find the slope of the line AC
\[{m_4} = \dfrac{{{y_c} - {y_a}}}{{x{}_c - {x_a}}} = \dfrac{{0 - \left( { - 2} \right)}}{{ - 1 - 2}} = \dfrac{2}{{ - 3}} = - \dfrac{2}{3}\]
Hence the slope of the line BE will be
\[{m_3} = - \dfrac{1}{{{m_4}}} = - \dfrac{1}{{ - \dfrac{2}{3}}} = \dfrac{3}{2}\]
So the equation of the line BE originating from vertex B (1, 1) and having slope \[{m_3} = \dfrac{3}{2}\] will be
\[
  y - {y_b} = {m_3}\left( {x - {x_b}} \right) \\
  y - 1 = \left( {\dfrac{3}{2}} \right)\left( {x - 1} \right) \\
  y - 1 = \dfrac{3}{2}x - \dfrac{3}{2} \\
  y = \dfrac{3}{2}x - \dfrac{3}{2} + 1 \\
  y = \dfrac{3}{2}x - \dfrac{1}{2} \\
 \]
Hence, the equation of the line BE \[y = \dfrac{3}{2}x - \dfrac{1}{2}\]
And Let CF be another altitude from vertex C and perpendicular to the line AB, where \[{m_5}\]and \[{m_6}\]are slope of the line CF and AB respectively and the lines are perpendicular to each other, where
\[
  {m_5} \times {m_6} = - 1 \\
  {m_5} = - \dfrac{1}{{{m_6}}} \\
 \]
Hence the slope\[{m_6}\] of the line AB will be
\[{m_6} = \dfrac{{{y_b} - {y_a}}}{{x{}_b - {x_a}}} = \dfrac{{1 - \left( { - 2} \right)}}{{1 - 2}} = \dfrac{3}{{ - 1}} = - 3\]
Where slope of the line CF will be
\[{m_5} = - \dfrac{1}{{{m_6}}} = - \dfrac{1}{{ - 3}} = \dfrac{1}{3}\]
So the equation of the line CF from the vertex C (-1, 0) with the slope \[{m_5} = \dfrac{1}{3}\] will be
\[
  y - {y_c} = {m_5}\left( {x - {x_c}} \right) \\
  y = \left( {\dfrac{1}{3}} \right)\left( {x + 1} \right) \\
  y = \dfrac{1}{3}x + \dfrac{1}{3} \\
 \]
Hence the equation of the line CF \[y = \dfrac{1}{3}x + \dfrac{1}{3}\].

Note: Candidates should be well aware about the coordinates of the vertices of the triangle before using the formula for the calculation of the slope of the line segment. The point of intersection of the altitudes of a triangle is known as the Orthocenter of the triangle and this can be only one specific point inside the triangle.