Question

Find the equation of a straight line that passes through $ \left( { - 2, - 7} \right) $ and has a length of intercept 3 between the straight lines whose equations are $ 4x + 3y = 12 $ and $ 4x + 3y = 3 $.

Answer 1

Hint: We should try to find the relation between the lines like they are parallel, perpendicular or any thing and most important is to draw their figure because it will help you a lot. We should be familiar with different formulas such as the distance between two parallel lines.

Complete Step By Step Answer:
The diagram of the question is

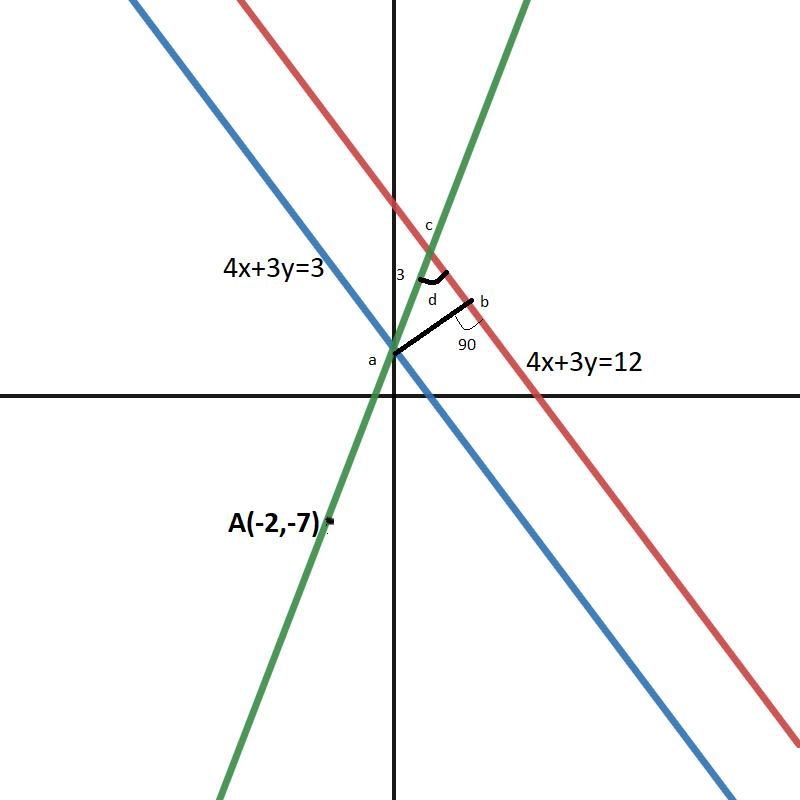
We have assumed the $ \angle acb = d $
We also construct line ab perpendicular lo parallel lines.
Now, we will find the distance between the two parallel lines by the formula,
 $ = \dfrac{{c1 - c2}}{{\sqrt {{a^2} + {b^2}} }} $
We will put the values and get
 $ = \dfrac{9}{5} $
Now, in triangle abc, by using Pythagoras theorem
 $ cb = {\sqrt {{3^2} - \left( {\dfrac{9}{5}} \right)} ^2} $
now, we will calculate the angle d,
 $ \tan d = \dfrac{{ab}}{{bc}} $
 $ = \dfrac{3}{4} $
Now, we will use the formula, to calculate the angle between two lines
 $ \tan d = \dfrac{{m1 - m2}}{{1 + m1 \times m2}} $
 $ \dfrac{3}{4} = \dfrac{{m + \dfrac{4}{3}}}{{1 - \dfrac{{4m}}{3}}} $
 $ m = - \dfrac{7}{{24}} $
So, the slope of the line, $ m = - \dfrac{7}{{24}} $
And this line is passing through $ \left( { - 2, - 7} \right) $ $ $
So, the equation of the line is $ (y + 7) = - (x + 2)\dfrac{7}{{24}} $ .

Note:
We should be familiar with different formulas like that of distance between two parallel lines. Drawing diagrams is an important step and try to draw correct diagrams, only by using diagrams can we solve half of the questions. Formulas are very important because they save time. Like in the above example, for the final equation of line we have slope and a point passing through so by using $ (y-{y_1}) = m(x-{x_1}) $ ,we calculated the equation easily.