Question

How do you find the equation of a sinusoidal graph?

Answer 1

Hint: In this question the objective is to find the equation of the sinusoidal graph. The sine angle in a right-angle triangle is the ratio perpendicular to the hypotenuse of the triangle.
\[\sin \theta = \dfrac{{perpendicular}}{{hypotenuse}}\].

Complete Step by Step solution:
As we know that the radian measure is defined as the ratio of the length of the circular arc to the radius of the arc, the measure of the angle is determined by the rotation from the initial side to the final side, and the angle is measured in degrees and in trigonometry the degree measure is \[\dfrac{1}{{{{360}^{{\text{th}}}}}}\] of the complete rotation.
The sinusoidal function is formed either by sine or cosine function. The general form of the sine wave is given by,
\[y = a\cos b\left( {x - c} \right) + d\]
In the above equation a is the amplitude of the graph that is defined as the deviation of the graph from the mean position.
The period of the graph is defined as the distance on the x axis before the function is repeated by itself, in case of the sinusoidal function the formula for it is \[\left( {2p} \right)\dfrac{i}{b}\].
To obtain the horizontal displacement is obtained by the formula \[x - c = 0\], here the horizontal displacement is the number of units by which the graph is displaced to the left or right from the x axis by some unit.
The vertical displacement d is the displacement of the graph by some units from the y axis.
Let us consider the table for the value of sine angle for different radian measures.
\[
  \sin 0 = 0 \\
  \sin \dfrac{\pi }{6} = \dfrac{1}{2} \\
  \sin \dfrac{\pi }{4} = \dfrac{1}{2} \\
  \sin \dfrac{\pi }{3} = \dfrac{{\sqrt 3 }}{2} \\
  \sin \pi = 1 \\
 \]
We will consider the following sinusoidal graph as,

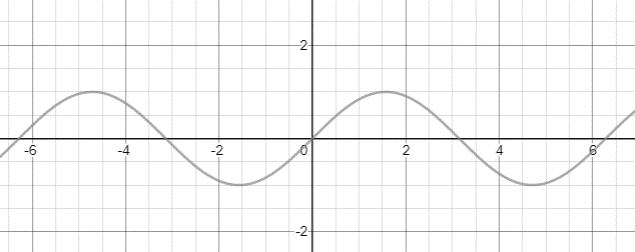
Note:
As we know that the trigonometry is the part of calculus and the basic ratio of trigonometric are sine and cosine which have their application in sound and light wave theories. The trigonometric have vast applications in naval engineering such as to determine the height of the wave and the tide in the ocean. Three important functions of trigonometry are sin, cosine and tangent.