Question

Find the eccentricity of the ellipse $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$ where B is an end point of a minor axis, S and S’ are foci such that $\vartriangle BSS'$ is an equilateral triangle.

Answer 1

Hint: Ellipse of the form $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$ is the one with semi major axis of length a parallel to x axis and semi minor with length b parallel to y axis. Eccentricity of an ellipse is the ratio of the distance between the centre and each focus of the ellipse to the semi major axis of the ellipse. That is $e = \dfrac{c}{a}$ . Or we have another formula to find the eccentricity e, ${e^2} = 1 - \dfrac{{{b^2}}}{{{a^2}}}$

Complete step-by-step answer:
Step 1: Let us represent the given data as a picture:
 

Step 2: Given that S and S’ are foci and B is the end point of the minor axis such that BSS’ forms an equilateral triangle. Thus our image will be,

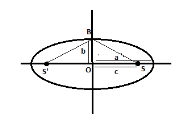
For an ellipse $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$, with semi minor axis length a and eccentricity e, the focus S=(ae,0) and S’=(-ae,0) and B=(0,b). As the triangle is equilateral, all three sides will be equal. Thus,
SS’=S’B implies ${(SS')^2} = {(S'B)^2}$ … Formula1
where SS’ is the distance between the foci which is ae+ae=2ae and applying Pythagoras theorem in the triangle OBS’, square of hypotenuse = sum of squares of base and altitude implies,
 $
  {(S'B)^2} = {(OS')^2} + {(OB)^2} \\
   = {(ae)^2} + {b^2} \\
 $
Thus formula1 will be reframed as, ${(2ae)^2} = {(ae)^2} + {b^2}$
Step 3: Simplifying the above we get,
 $
  4{(ae)^2} - {(ae)^2} = {b^2} \\
  3{a^2}{e^2} = {b^2} \\
 $
As we need the eccentricity e, we solve with respect to e.
$3{e^2} = \dfrac{{{b^2}}}{{{a^2}}}$ … Formula2
Step 4: Recalling the formula for eccentricity of an ellipse $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$,
 ${e^2} = 1 - \dfrac{{{b^2}}}{{{a^2}}}$… Formula 3
Substituting Formula 2 in Formula 3 we get, ${e^2} = 1 - 3{e^2}$
Implies
$
  4{e^2} = 1 \\
  e = \sqrt {\dfrac{1}{4}} \\
 $
$e = \dfrac{1}{2}$

Final Answer: Eccentricity , $e = \dfrac{1}{2}$

Note: Other form of ellipse is $\dfrac{{{x^2}}}{{{b^2}}} + \dfrac{{{y^2}}}{{{a^2}}} = 1$with the major axis along y axis and minor along x axis. Its foci will be (0, ae) and (0, -ae). Thus in general, the ellipse centred at (h, k) can be represented by the formula$\dfrac{{{{(x - h)}^2}}}{{{a^2}}} + \dfrac{{{{(y - k)}^2}}}{{{b^2}}} = 1$ or vise versa according to the axis where the ellipse is oriented.