Question

How do you find the domain and range of, $f\left( x,y \right)=\sqrt{9-{{x}^{2}}-{{y}^{2}}}$ ?

Answer 1

Hint: The given function is not a function in just one variable, but a function in two variables. Also, we will first find the domain of the given expression and then find its corresponding range. Since, the given expression is a square root function, we will start by equating the term inside the square root as greater than or equal to zero. We shall proceed in this manner to get our final solution.

Complete step by step solution:
We shall first find the domain of the given function. The function given to us in the problem is,
$\Rightarrow f\left( x,y \right)=\sqrt{9-{{x}^{2}}-{{y}^{2}}}$
Here, for the square root function to be operational, the term inside the square root should be greater than or equal to zero. This can be used to calculate the domain of the function as follows:
$\begin{align}
  & \Rightarrow \sqrt{9-{{x}^{2}}-{{y}^{2}}}\ge 0 \\
 & \Rightarrow 9-{{x}^{2}}-{{y}^{2}}\ge 0 \\
 & \Rightarrow 9\ge {{x}^{2}}+{{y}^{2}} \\
 & \Rightarrow {{3}^{2}}\ge {{x}^{2}}+{{y}^{2}} \\
\end{align}$
From our above calculation, we can see that the domain of the given function is the region inside the circle with center at (0,0) and having a radius of 3 units. The domain thus, can be represented with the help of the following shaded circle diagram:

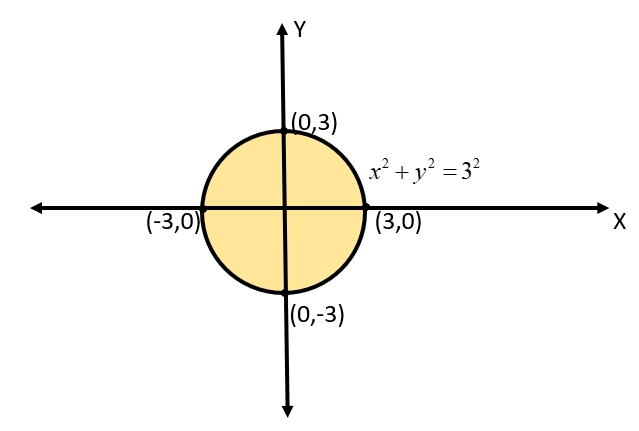
Now that we have the domain of our function, we can calculate the range of the function. This can be done by plotting the image of this circle over the Y-axis and collecting all the points. On doing so, we get the range of our function as:
$\Rightarrow R=\left[ -3,3 \right]$
But, since the square root function always yields a positive value, our range will not take all the negative values. Thus, our final range comes out to be :
$\Rightarrow {{R}_{final}}=\left[ 0,3 \right]$

Hence, the domain of the function, $f\left( x,y \right)=\sqrt{9-{{x}^{2}}-{{y}^{2}}}$ comes out to be ${{x}^{2}}+{{y}^{2}}\le {{3}^{2}}$ and the range of the function comes out to be [0,3].

Note:
While calculating the range of any square root function, one needs to be careful while writing the final answer as the square root function always yields a non-negative value only, until unless specified. Also, the use of diagrams sometimes makes our problem easier to understand and calculate.