Question

Find the domain and range of $f\left( g\left( x \right) \right)$ where
$f\left( x \right)=\left\{ \begin{matrix}
   x+1 & \text{if }x\le 1 \\
   2x+1 & \text{if }1 < x \le 2 \\
\end{matrix} \right.,g\left( x \right)=\left\{ \begin{matrix}
   {{x}^{2}} & \text{if }-1 < x \le 2 \\
   x+2 & \text{if 2}\le x\le 3 \\
\end{matrix} \right.$ \[\]

Answer 1

Hint: We take the intersection of domains of $f\left( x \right)$ and $g\left( x \right)$ to find the domain of $f\left( g\left( x \right) \right)$. We put $g\left( x \right)$ in place of $x$ in the given definition of function $f\left( x \right)$ and considering obtained domain, using the domain of $f\left( x \right)$ and the definition $g\left( x \right)$ under the limits to define $f\left( g\left( x \right) \right)$. We find the range of $f\left( g\left( x \right) \right)$ checking the value of $f\left( g\left( x \right) \right)$ at the limits of interval. \[\]

Complete step-by-step answer:
We know that if $f\left( x \right):A\to B,g\left( x \right):B\to C$ are two functions then the composite function $fog\left( x \right)$ is defined as $f\left( g\left( x \right) \right)=B\to A$.
We are given two piecewise defined functions $f\left( x \right)$ and $g\left( x \right)$ as defined below.
\[\begin{align}
  & f\left( x \right)=\left\{ \begin{matrix}
   x+1 & \text{if }x\le 1 \\
   2x+1 & \text{if }1 < x \le 2 \\
\end{matrix} \right. \\
 & g\left( x \right)=\left\{ \begin{matrix}
   {{x}^{2}} & \text{if }-1 < x \le 2 \\
   x+2 & \text{if } 2 < x\le 3 \\
\end{matrix} \right. \\
\end{align}\]
We see that piecewise function $f\left( x \right)$ is defined for $x \le 1$ and $1 < x \le 2$ which means it has the domain
\[x\in \left( -\infty ,1 \right]\bigcup \left( 1,2 \right]=\left( -\infty ,2 \right]....\left( 1 \right)\]
 Similarly the piecewise defined function $g\left( x \right)$ is defined for $-1 < x \le 2$ and $2 < x\le 3$,which means it has the domain
\[x\in \left[ -1,2 \right)\bigcup \left[ 2,3 \right]=\left[ -1,3 \right].....\left( 2 \right)\]
We are asked to find the domain and range of their composite function $f\left( g\left( x \right) \right)$. The definition of $g\left( x \right)$ is limited by its domain$\left[ -1,2 \right]$ and the definition of $f\left( x \right)$is limited by its domain$\left( -\infty ,2 \right]$. So the domain of $f\left( g\left( x \right) \right)$ will be the intersection of domains of $f\left( x \right)$ and $g\left( x \right)$ which is
\[ x \in \left[ -1,3 \right]\bigcap \left( -\infty ,2 \right]=\left[ -1,2 \right]\]
Let us put $g\left( x \right)$ in place of $x$ in the definition of $f\left( x \right)$ to get the definition of$f\left( g\left( x \right) \right)$.So we have;
\[f\left( g\left( x \right) \right)=\left\{ \begin{matrix}
   g\left( x \right)+1 & \text{if }x\le 1 \\
   2g\left( x \right)+1 & \text{if }1 < x\le 2 \\
\end{matrix} \right...........\left( 3 \right)\]
We see that the function $f\left( g\left( x \right) \right)$ will have different two sub-functions before and after $x=1$ because $f\left( x \right)$ has two sub-functions before and after$x=1$. So we put $g\left( x \right)={{x}^{2}}$ in (3) for $-1\le x\le 1$ and $1 < x\le 2$ in (1) since $g\left( x \right)={{x}^{2}}$ for all $-1\le x\le 2$ and define $f\left( g\left( x \right) \right)$ as
\[f\left( g\left( x \right) \right)=\left\{ \begin{matrix}
   {{x}^{2}}+1 & \text{if }-1 < x\le 1 \\
   2{{x}^{2}}+1 & \text{if }1 < x \le 2 \\
\end{matrix} \right.\]
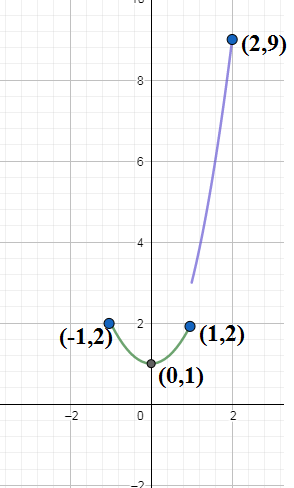
We see that when $-1\le x\le 1$ then we have
\[\begin{align}
  & 0\le {{x}^{2}}\le 1 \\
 & \Rightarrow 1\le {{x}^{2}}+1\le 2 \\
 & \Rightarrow 1\le f\left( g\left( x \right) \right)\le 2 \\
 & \Rightarrow f\left( g\left( x \right) \right)\in \left[ 1,2 \right].......\left( 4 \right) \\
\end{align}\]
We also observe that when $1\le x\le 2$ then we have
\[\begin{align}
  & 1 < {{x}^{2}}\le 4 \\
 & \Rightarrow 2\cdot 1+1<2{{x}^{2}}+1\le 2\cdot 4+1 \\
 & \Rightarrow 3 < f\left( g\left( x \right) \right)\le 9 \\
 & \Rightarrow f\left( g\left( x \right) \right)\in \left( 3,9 \right].....\left( 5 \right) \\
\end{align}\]
We take union of the intervals in (4) and (5) and find the required range as
\[f\left( g\left( x \right) \right)\in \left[ 1,2 \right]\bigcup \left( 3,9 \right]\]

Note: We note that a piecewise has different functions in different intervals and each function is called a sub function. We also note that the sub-function $g\left( x \right)=2$ could not be used since $f\left( g\left( x \right) \right)$ is not denied for $x>2$. We must be careful of the less than and less than equal to sign as well as greater than or greater than equal to sign while solving this problem.