
Find the distance of the point \[P\left( -1,-5,-10 \right)\] from the point of intersection of the line \[\overrightarrow{r}=\left( 2\widehat{i}-\widehat{j}+2\widehat{k} \right)+\lambda \left( 3\widehat{i}+3\widehat{j}+2\widehat{k} \right)\] and the plane \[\overrightarrow{r}.\left( \widehat{i}-\widehat{j}+\widehat{k} \right)=5\]?
Answer
563.7k+ views
Hint: We start solving the problem by assuming \[\overrightarrow{r}=x\widehat{i}+y\widehat{j}+z\widehat{k}\] and then find the general form of all the points that lie on the line given in the problem. We then find the equation of the plane by making use of the fact that \[\left( a\widehat{i}+b\widehat{j}+c\widehat{k} \right).\left( d\widehat{i}+e\widehat{j}+f\widehat{k} \right)=\left( a\times d \right)+\left( b\times e \right)+\left( c\times f \right)\]. We then subtract the obtained general form of the point in the equation of the plane to find the value of $ \lambda $ , which helps us to find the intersection point. We then find the between the obtained intersection point and \[P\left( -1,-5,-10 \right)\] by making use of the fact that the distance between the points $ \left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right) $ and $ \left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right) $ is $ \sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}+{{\left( {{z}_{2}}-{{z}_{1}} \right)}^{2}}} $ .
Complete step by step answer:
According to the problem, we are asked to find the distance of the point \[P\left( -1,-5,-10 \right)\] from the point of intersection of the line \[\overrightarrow{r}=\left( 2\widehat{i}-\widehat{j}+2\widehat{k} \right)+\lambda \left( 3\widehat{i}+3\widehat{j}+2\widehat{k} \right)\] and the plane \[\overrightarrow{r}.\left( \widehat{i}-\widehat{j}+\widehat{k} \right)=5\].
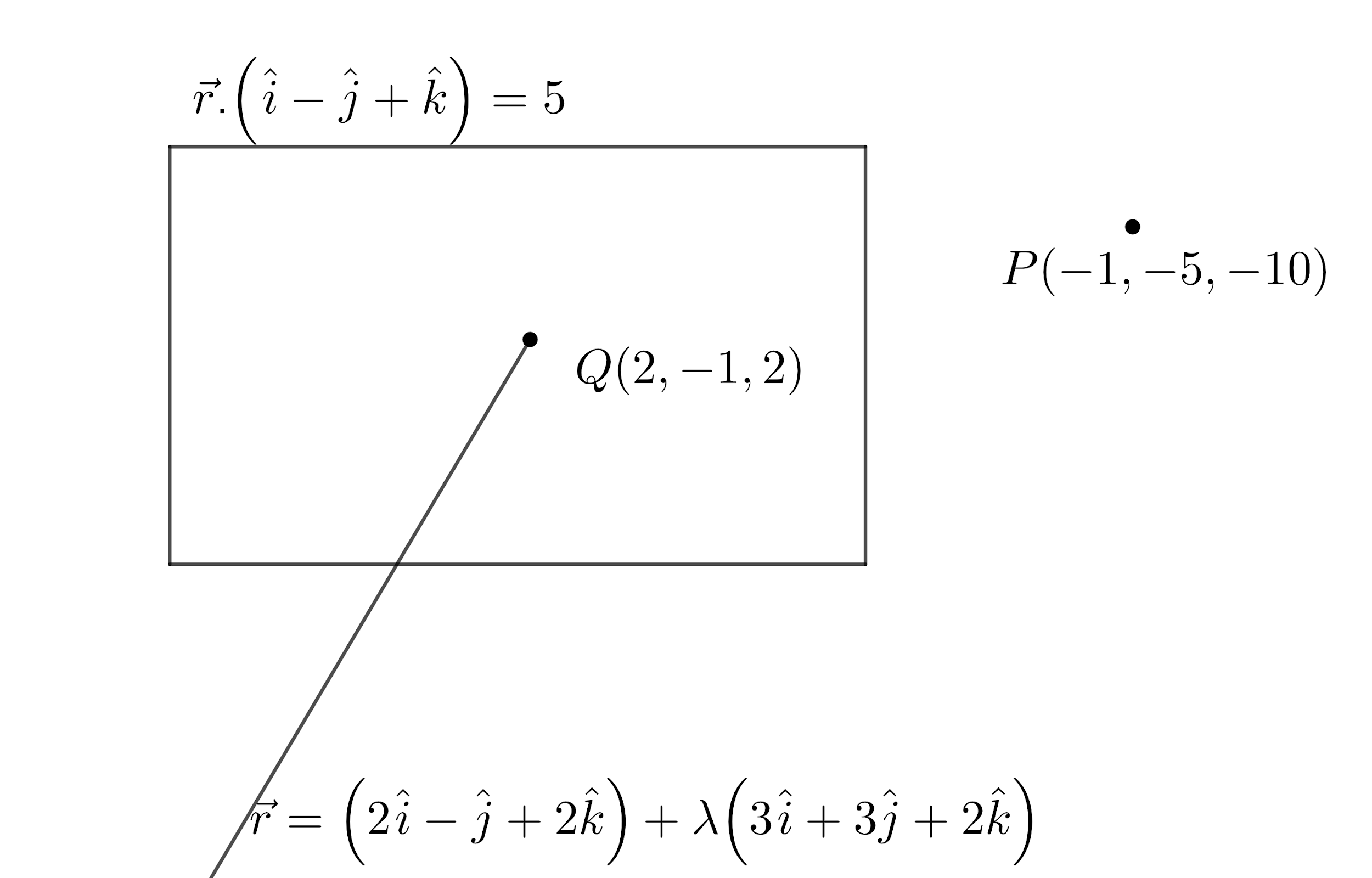
Let us assume \[\overrightarrow{r}=x\widehat{i}+y\widehat{j}+z\widehat{k}\].
So, the point of the lines can be represented as \[x\widehat{i}+y\widehat{j}+z\widehat{k}=\left( 2\widehat{i}-\widehat{j}+2\widehat{k} \right)+\lambda \left( 3\widehat{i}+3\widehat{j}+2\widehat{k} \right)\].
$ \Rightarrow x\widehat{i}+y\widehat{j}+z\widehat{k}=\left( \left( 2+3\lambda \right)\widehat{i}+\left( -1+3\lambda \right)\widehat{j}+\left( 2+2\lambda \right)\widehat{k} \right) $ .
Comparing corresponding elements on both sides, we get the general form of all the points lying on the given line as $ \left( 2+3\lambda,-1+3\lambda,2+2\lambda \right) $ ---(1).
Now, let us find the equation of the plane \[\overrightarrow{r}.\left( \widehat{i}-\widehat{j}+\widehat{k} \right)=5\].
So, we have \[\left( x\widehat{i}+y\widehat{j}+z\widehat{k} \right).\left( \widehat{i}-\widehat{j}+\widehat{k} \right)=5\].
We know that \[\left( a\widehat{i}+b\widehat{j}+c\widehat{k} \right).\left( d\widehat{i}+e\widehat{j}+f\widehat{k} \right)=\left( a\times d \right)+\left( b\times e \right)+\left( c\times f \right)\].
So, the equation of the plane is \[x-y+z=5\] ---(2).
Let us substitute equation (1) in equation (2) to get the value of $ \lambda $ which helps us to find the point of intersection of line and plane.
So, we have \[\left( 2+3\lambda \right)-\left( -1+3\lambda \right)+\left( 2+2\lambda \right)=5\].
\[\Rightarrow 2+3\lambda +1-3\lambda +2+2\lambda =5\].
\[\Rightarrow 5+2\lambda =5\].
\[\Rightarrow 2\lambda =0\].
\[\Rightarrow \lambda =0\] ---(3).
Let us substitute equation (3) in equation (1) to get the point of intersection of line and plane.
So, we have $ Q\left( 2+3\left( 0 \right),-1+3\left( 0 \right),2+2\left( 0 \right) \right)=Q\left( 2,-1,2 \right) $ .
Now, let us find the distance between the points \[P\left( -1,-5,-10 \right)\] and \[Q\left( 2,-1,2 \right)\].
We know that the distance between the points $ \left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right) $ and $ \left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right) $ is $ \sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}+{{\left( {{z}_{2}}-{{z}_{1}} \right)}^{2}}} $ .
So, the distance between points P and Q is $ PQ=\sqrt{{{\left( 2+1 \right)}^{2}}+{{\left( -1+5 \right)}^{2}}+{{\left( 2+10 \right)}^{2}}} $ .
$ \Rightarrow PQ=\sqrt{{{\left( 3 \right)}^{2}}+{{\left( 4 \right)}^{2}}+{{\left( 12 \right)}^{2}}} $ .
$ \Rightarrow PQ=\sqrt{9+16+144} $ .
$ \Rightarrow PQ=\sqrt{169} $ .
$ \Rightarrow PQ=13 $ units.
$ \therefore $ We have found the distance of the point \[P\left( -1,-5,-10 \right)\] from the point of intersection of the line \[\overrightarrow{r}=\left( 2\widehat{i}-\widehat{j}+2\widehat{k} \right)+\lambda \left( 3\widehat{i}+3\widehat{j}+2\widehat{k} \right)\] and the plane \[\overrightarrow{r}.\left( \widehat{i}-\widehat{j}+\widehat{k} \right)=5\] as 13 units.
Note:
We can see that the given problems contain huge amounts of calculations, so we need to perform each step carefully to avoid confusion and calculation mistakes. Whenever we get this type of problem, we first try to find the general form to represent all the points on the line. We can also find the value of $ \lambda $ as shown below:
$ \Rightarrow \overrightarrow{r}.\left( \widehat{i}-\widehat{j}+\widehat{k} \right)=\left( \left( 2\widehat{i}-\widehat{j}+2\widehat{k} \right)+\lambda \left( 3\widehat{i}+3\widehat{j}+2\widehat{k} \right) \right).\left( \widehat{i}-\widehat{j}+\widehat{k} \right) $ .
$ \Rightarrow \overrightarrow{r}.\left( \widehat{i}-\widehat{j}+\widehat{k} \right)=\left( 2\widehat{i}-\widehat{j}+2\widehat{k} \right).\left( \widehat{i}-\widehat{j}+\widehat{k} \right)+\lambda \left( 3\widehat{i}+3\widehat{j}+2\widehat{k} \right).\left( \widehat{i}-\widehat{j}+\widehat{k} \right) $ .
$ \Rightarrow 5=\left( 2+1+2 \right)+\lambda \left( 3-3+2 \right) $ .
$ \Rightarrow 5=5+2\lambda $ .
$ \Rightarrow 2\lambda =0 $ .
$ \Rightarrow \lambda =0 $ .
Complete step by step answer:
According to the problem, we are asked to find the distance of the point \[P\left( -1,-5,-10 \right)\] from the point of intersection of the line \[\overrightarrow{r}=\left( 2\widehat{i}-\widehat{j}+2\widehat{k} \right)+\lambda \left( 3\widehat{i}+3\widehat{j}+2\widehat{k} \right)\] and the plane \[\overrightarrow{r}.\left( \widehat{i}-\widehat{j}+\widehat{k} \right)=5\].
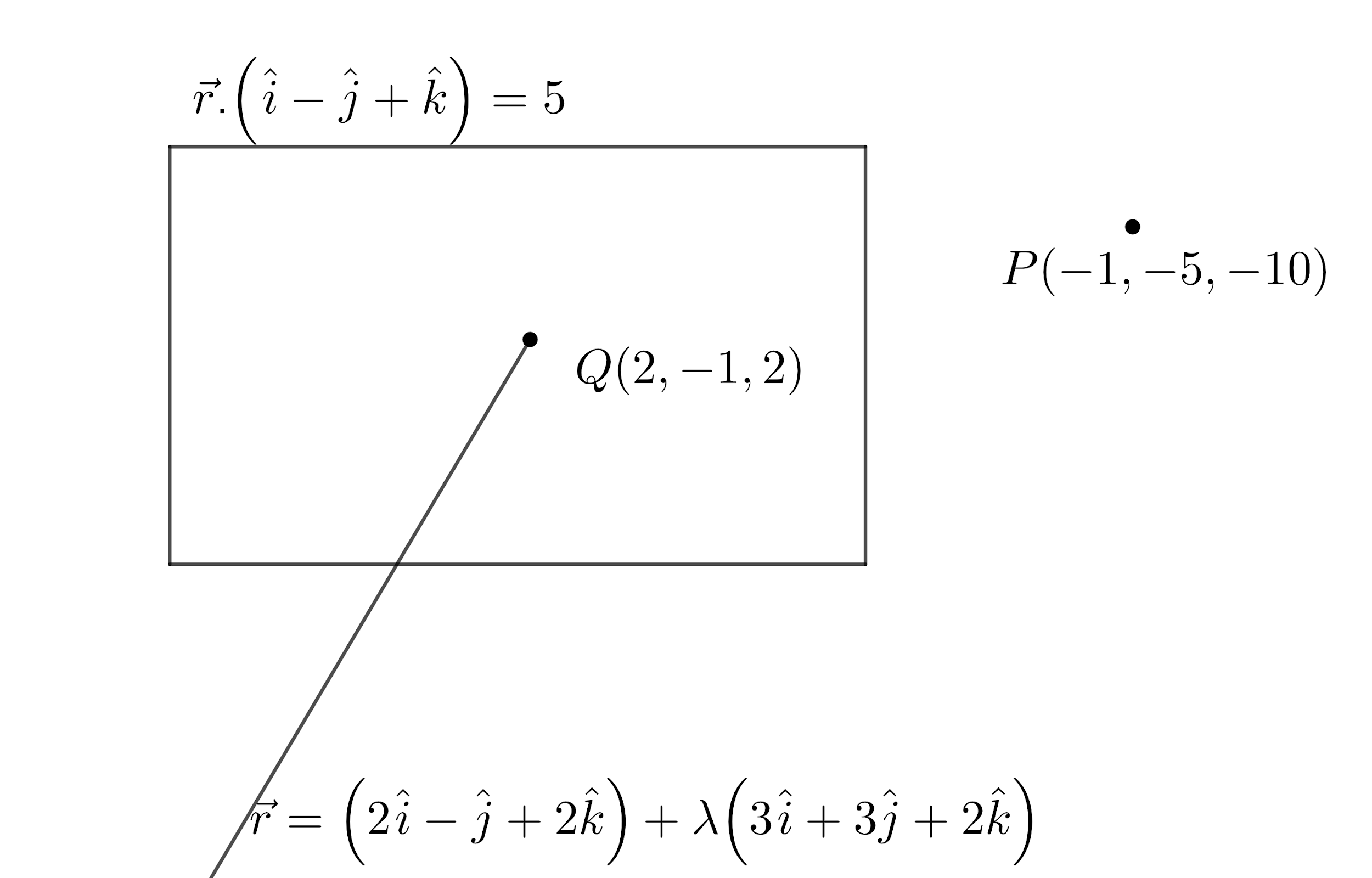
Let us assume \[\overrightarrow{r}=x\widehat{i}+y\widehat{j}+z\widehat{k}\].
So, the point of the lines can be represented as \[x\widehat{i}+y\widehat{j}+z\widehat{k}=\left( 2\widehat{i}-\widehat{j}+2\widehat{k} \right)+\lambda \left( 3\widehat{i}+3\widehat{j}+2\widehat{k} \right)\].
$ \Rightarrow x\widehat{i}+y\widehat{j}+z\widehat{k}=\left( \left( 2+3\lambda \right)\widehat{i}+\left( -1+3\lambda \right)\widehat{j}+\left( 2+2\lambda \right)\widehat{k} \right) $ .
Comparing corresponding elements on both sides, we get the general form of all the points lying on the given line as $ \left( 2+3\lambda,-1+3\lambda,2+2\lambda \right) $ ---(1).
Now, let us find the equation of the plane \[\overrightarrow{r}.\left( \widehat{i}-\widehat{j}+\widehat{k} \right)=5\].
So, we have \[\left( x\widehat{i}+y\widehat{j}+z\widehat{k} \right).\left( \widehat{i}-\widehat{j}+\widehat{k} \right)=5\].
We know that \[\left( a\widehat{i}+b\widehat{j}+c\widehat{k} \right).\left( d\widehat{i}+e\widehat{j}+f\widehat{k} \right)=\left( a\times d \right)+\left( b\times e \right)+\left( c\times f \right)\].
So, the equation of the plane is \[x-y+z=5\] ---(2).
Let us substitute equation (1) in equation (2) to get the value of $ \lambda $ which helps us to find the point of intersection of line and plane.
So, we have \[\left( 2+3\lambda \right)-\left( -1+3\lambda \right)+\left( 2+2\lambda \right)=5\].
\[\Rightarrow 2+3\lambda +1-3\lambda +2+2\lambda =5\].
\[\Rightarrow 5+2\lambda =5\].
\[\Rightarrow 2\lambda =0\].
\[\Rightarrow \lambda =0\] ---(3).
Let us substitute equation (3) in equation (1) to get the point of intersection of line and plane.
So, we have $ Q\left( 2+3\left( 0 \right),-1+3\left( 0 \right),2+2\left( 0 \right) \right)=Q\left( 2,-1,2 \right) $ .
Now, let us find the distance between the points \[P\left( -1,-5,-10 \right)\] and \[Q\left( 2,-1,2 \right)\].
We know that the distance between the points $ \left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right) $ and $ \left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right) $ is $ \sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}+{{\left( {{z}_{2}}-{{z}_{1}} \right)}^{2}}} $ .
So, the distance between points P and Q is $ PQ=\sqrt{{{\left( 2+1 \right)}^{2}}+{{\left( -1+5 \right)}^{2}}+{{\left( 2+10 \right)}^{2}}} $ .
$ \Rightarrow PQ=\sqrt{{{\left( 3 \right)}^{2}}+{{\left( 4 \right)}^{2}}+{{\left( 12 \right)}^{2}}} $ .
$ \Rightarrow PQ=\sqrt{9+16+144} $ .
$ \Rightarrow PQ=\sqrt{169} $ .
$ \Rightarrow PQ=13 $ units.
$ \therefore $ We have found the distance of the point \[P\left( -1,-5,-10 \right)\] from the point of intersection of the line \[\overrightarrow{r}=\left( 2\widehat{i}-\widehat{j}+2\widehat{k} \right)+\lambda \left( 3\widehat{i}+3\widehat{j}+2\widehat{k} \right)\] and the plane \[\overrightarrow{r}.\left( \widehat{i}-\widehat{j}+\widehat{k} \right)=5\] as 13 units.
Note:
We can see that the given problems contain huge amounts of calculations, so we need to perform each step carefully to avoid confusion and calculation mistakes. Whenever we get this type of problem, we first try to find the general form to represent all the points on the line. We can also find the value of $ \lambda $ as shown below:
$ \Rightarrow \overrightarrow{r}.\left( \widehat{i}-\widehat{j}+\widehat{k} \right)=\left( \left( 2\widehat{i}-\widehat{j}+2\widehat{k} \right)+\lambda \left( 3\widehat{i}+3\widehat{j}+2\widehat{k} \right) \right).\left( \widehat{i}-\widehat{j}+\widehat{k} \right) $ .
$ \Rightarrow \overrightarrow{r}.\left( \widehat{i}-\widehat{j}+\widehat{k} \right)=\left( 2\widehat{i}-\widehat{j}+2\widehat{k} \right).\left( \widehat{i}-\widehat{j}+\widehat{k} \right)+\lambda \left( 3\widehat{i}+3\widehat{j}+2\widehat{k} \right).\left( \widehat{i}-\widehat{j}+\widehat{k} \right) $ .
$ \Rightarrow 5=\left( 2+1+2 \right)+\lambda \left( 3-3+2 \right) $ .
$ \Rightarrow 5=5+2\lambda $ .
$ \Rightarrow 2\lambda =0 $ .
$ \Rightarrow \lambda =0 $ .
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

The draft of the Preamble of the Indian Constitution class 10 social science CBSE

Who gave "Inqilab Zindabad" slogan?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths




