Question

Find the distance of a chord 8cm from the center of the circle of radius 5 cm .
A. 2 cm
B. 3 cm
C. 4 cm
D. 6 cm

Answer 1

Hint: In this problem, we are given a circle having center O with a chord AB. Length of the chord AB is 8 cm and the radius of circle i.e. OA is 5 cm. By visualizing the diagram, we can easily solve our problem and find the distance of OP.

Complete step-by-step answer:

Consider a circle having center O with a chord. Let OA be the radius of the circle and AB be the chord. As given in the question, the radius of the circle is 5 cm and length of chord is 8 cm. Let the distance between the center of the circle and chord be OP. So, this can be shown diagrammatically as:

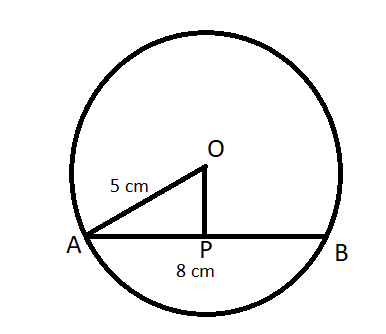
It is clear from the diagram that OP is perpendicular to AB. As OP is perpendicular to AB and passes through the center O, it will bisect the chord AB at P. Now the length of AP will be,
$\begin{align}
  & AP=\dfrac{1}{2}\times AB \\
 & AP=\dfrac{1}{2}\times 8 \\
 & AP=4cm \\
\end{align}$
Since, triangle OPA is a right-angle triangle, we can easily apply the Pythagoras theorem which can be stated as ${{b}^{2}}+{{p}^{2}}={{h}^{2}}$ where b, p and h are base, perpendicular and hypotenuse of the respective triangle.
$\begin{align}
  & \text{In }\Delta OPA, \\
 & A{{P}^{2}}+O{{P}^{2}}=A{{O}^{2}} \\
 & O{{P}^{2}}=A{{O}^{2}}-A{{P}^{2}} \\
 & O{{P}^{2}}={{5}^{2}}-{{4}^{2}} \\
 & OP=\sqrt{25-16} \\
 & OP=\sqrt{9}=3cm \\
\end{align}$
Therefore, the distance of the chord AB from the center is 3 cm.
Hence, option (b) is correct.

Note: The key step for solving this problem is transforming the statement into a diagram. Once the diagram is known, then we can easily evaluate the required thing. Students must be careful in drawing the diagram and labelling it.