Question

Find the distance between the parallel planes \[x+y-z+4=0\] and \[x+y-z+5=0\]
(a) \[\dfrac{10}{3\sqrt{3}}\]
(b) \[\dfrac{10}{9}\]
(c) \[\dfrac{1}{\sqrt{3}}\]
(d) \[\dfrac{3}{10}\]

Answer 1

Hint: In this question, we first need to compare the given two plane equations with the general form of two parallel places given by \[ax+by+cz+{{d}_{1}}=0\] and \[ax+by+cz+{{d}_{2}}=0\]. Now, get the values of the coefficients on comparing. Then, use the formula for distance between two parallel planes which is given by \[\left| \dfrac{{{d}_{2}}-{{d}_{1}}}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}} \right|\]. Now, on further simplification we get the result.

Complete step by step answer:
Equation of a Plane Parallel to a given Plane
Cartesian Form:
The Cartesian equation of a plane parallel to the given plane is given by \[ax+by+cz+{{d}_{1}}=0\] is \[ax+by+cz+{{d}_{2}}=0\]
Distance between two Parallel Planes:
If \[ax+by+cz+{{d}_{1}}=0\] and \[ax+by+cz+{{d}_{2}}=0\] be equation of two parallel planes. Then, the distance between them is
\[\left| \dfrac{{{d}_{2}}-{{d}_{1}}}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}} \right|\]
Now, the equation of parallel planes in the question are
\[\Rightarrow x+y-z+4=0,x+y-z+5=0\]
Now, on comparing these given parallel planes with the general form of two parallel planes given by \[ax+by+cz+{{d}_{1}}=0,ax+by+cz+{{d}_{2}}=0\] we get,
\[a=1,b=1,c=-1,{{d}_{1}}=4,{{d}_{2}}=5\]
As we already know that the distance between two parallel planes is given by the formula
\[\Rightarrow \left| \dfrac{{{d}_{2}}-{{d}_{1}}}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}} \right|\]
Now, on substituting the respective values of the coefficients in the above formula we get,
\[\Rightarrow \left| \dfrac{5-4}{\sqrt{{{1}^{2}}+{{1}^{2}}+{{\left( -1 \right)}^{2}}}} \right|\]
Now, this can be further written in the simplified form as
\[\Rightarrow \left| \dfrac{1}{\sqrt{{{1}^{2}}+{{1}^{2}}+{{\left( -1 \right)}^{2}}}} \right|\]
Now, on simplifying this further we get,
\[\Rightarrow \left| \dfrac{1}{\sqrt{1+1+1}} \right|\]
Now, this can be further written on further simplification as
\[\Rightarrow \left| \dfrac{1}{\sqrt{3}} \right|\]
As it is a positive value we can remove the mod and write it as
\[\Rightarrow \dfrac{1}{\sqrt{3}}\]
Hence, the correct option is (c).

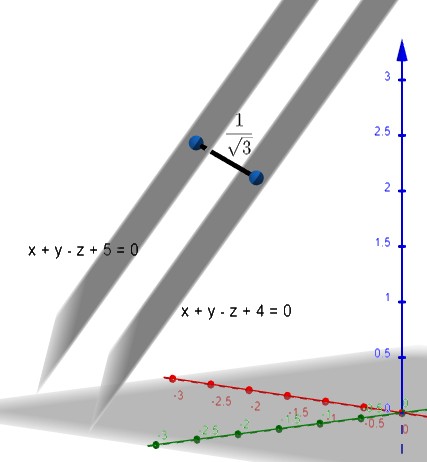
Note: Instead of using the formula for the distance between the two parallel planes, we can also solve it by considering any of the points on any of the planes and find the distance between that point and the other plane. Both the methods give the same result but it is suggestable to use the direct formula for distance two parallel planes.
It is important to note that while comparing the coefficients we should not neglect any of the term or interchange the values because it completely changes the final result.